для полосковых линии

Z(P)=: j (Р(р)-Г„(р, p)-34p)dSdS, (1.3;

длящелевыхлиний

*>(Р) = j j J4p)-T22(p. p)-r{p)dSdS, (1.3:

где J, J - функции распределения поверхностных плотностей электрическог и магнитного токов на полоске или в щели; Гц, Ггг--тензорные функции Fpi на электрического и магнитного типов соответствующих структур, записаннн так, что их характеристические части связаны с осью z (см. § 1.3).

Использование в (1.31), (1.32) аппроксимирующих токовых функций впд

приводит к дисперсионным уравнениям для определения постоянных распр. странения р.

Для полосковых ЛП

Для численного решения дисперсионных уравнений используют различные итерационные процедуры: метод Ньютона, метод секущих и др. Затраты машинного времени при определении корней зависят, в частности, от удачного выбора начального приближения. В качестве такого приближения для основного типа волиы .может служить квазистатическое решение (1.35) или более точные представления, о которых будет сказано ниже.

В практике расчета режимов ПЛП с основны.м типсм колебаний широко применяют понятия эффективной диэлектрической проницаемости и характеристического сопротивления, получаемые на основе решения уравнений Лапласа для соответствующих граничных задач. Формулы для расчета еэф и Zc могут быть полезны и при анализе полосковых антенн. Так, в [65], получены следующие выражения для эффективной проницаемости МПЛ (см. рис. 1.4,6), обеспечивающие точность 1% (0,05<sy/d<20; ej<:16):

е,ф=(<+ 1)/2 + (е;-1)[(1 + 12й?/ ;)->2 + 0,04(1-ге;/)]/2. Wld<l;

вф-(; + 1)/2 + (е;-1)(1-4-12 >/2/2. wid>l. (1.36)

Такую же точность дают следующие формулы для характеристического сопротивления, выраженного в омах:

+

Для щелевых линий

L У (0) г^(0) J

(1.33

V2 (s;+i)

(1.34

Здесь для экранированной линии (см. рис. 1.4,а)

Y (0) = - /т, Ctg - /f2 ctg

(0) = - /(OEi ctg -Ifirf/lf, - /ШЕ2 ctg 722,Т2.

для МПЛ (см. рис. 1.4,6)

Y {0) = - /if, Ctg Tid/< li -h T2>[. (0) = -ушЕ, ctg 7,аГ/т, -f ше/г,

Для линий, изображенных на рис. 1.4,в, г, проводимости, входящие в ди персионные уравнения, определяют путем рекуррентных пересчетов от сто к слою по (1.22).

Полагая в (1.33) о->-0, можно получить приближенное решение для постг янной распространения. Так, для МПЛ

е; -1

0,2258 +

0,1208 \

v< \ 2d

wld<\b\

<+1

+ 0,4413-Ь

0,0823 (s;--. 1)

0,2310 + 0.15921 -+0

/flr>3,3. (1.37)

(1.35

Аналогичные результаты получены в квазистатическом приближении и для других распространенных типов линий. Например, для щелевой линии (см. рис. 1.4,г) расчетные формулы для постоянной распространения и характеристического сопротивления можно найти в [31, 32].

ГЛАВА 2.

ИЗЛУЧЕНИЕ ЛИНЕЙНЫХ МИКРОПОЛОСКОВЫХ АНТЕНН

2.1. ОБЗОР МЕТОДОВ РАСЧЕТА МПА

Как отмечалось во введении, микрополосковые антенны широко распространены в качестве излучателей дециметрового, сантиметрового и миллиметрового диапазонов длин волн. Этому спо-

собствовали простота конструкции, высокая технологичность, м, лентного ей волновода. Наибольшее распространение этот метол лая масса, повторяемость размеров, низкая стоимость изготовлю получил при расчете эквивалентных параметров неоднородностеи ния и др. Хорошие аэродинамические качества позволяют успешн в линиях, однако он применим и при анализе антенн, выполнен-использовать антенны этого типа на высокоскоростных летател ных на базе полосковых линий. Полосковая антенна заменяется ных аппаратах, а также в качестве излучающих элементов фаз1 отрезком волновода и ее излучение определяется как излучение рованных антенных решеток (ФАР), в системах с электрически торцов волновода [1, 14, 33]. По принятому распределению тока на сканированием луча. Широкому распространению МПА содейст торцах определяется векторный потенциал, через который выра-вовало появление новых типов диэлектриков, обладающих ма жаются компоненты поля в дальней зоне.

лыми потерями и высокой степенью однородности материале Существенные расхождения теоретических расчетов и экспери-Наличие диэлектрика позволяет существенно уменьшить линейны ментальных измерений привели к тому, что некоторые исследова-размеры излучающих элементов и использовать их при созданш теля пошли по пути создания методов определения характеристик миниатюрных антенных систем. Однако присутствие этого покры МПА; имеющих синтетический характер, т. е. таких, при которых тия и связанных с ним поверхностных волн существенно услск в теоретических расчетах используются параметры, определяемые няет определение характеристик излучения МПА В связи со стол экспериментально. Примером такого подхода может служить 134J. ностью механизма излучения МПА, трудностями эксперименталь ДрУГОЙ метод нахождения характеристик излучения полосковых ной отладки их образцов значительно возрастает роль расчетные антенн заключается в разбиении полупространства, ограниченного методов, основанных на строгих подходах и дающих необходимук проводящим экраном со слоем диэлектрика, на несколько обла-для инженерной практики точность расчета основных характери стей с постоянными параметрами и определении потенциала для стик. К настоящему времени известно достаточно большое числе каждой из этих областей с учетом выполнения граничных условии методов расчета антенн рассматриваемого типа между ними [35]. В свою очередь компоненты возбуждаемого поля

Один из первых методов расчета характеристик излучения определяются через найденный потенциал. Диаграмма направлен-МПА основан hS представленииЧрямоуголГно^антенн рассчитывается как результат излучения двухэлементной

ми аХЬ в виде двух Магнитных виаторов-щелей разчны Р^ элементом которой является отрезок полосковои на расстояние b друг от друга [8, 24]. Связь излучадхщелё,! Ш^-го зеркальное изображение на эк-по внутреннему пространству осуществляется введением соединяю Р^

щего отрезка линии с постоянной распространения 6 и харак- Указанным методом свойствен общий недостаток - косвенный теристическим сопротивлением Z определяемых шириной антен-У' диэлектрика и, как следствие, отсутствие какой-либо ны. Полагают, что линия поддерживает только квази-Т волну Б информации о поверхностных волнах, возбуждаемых в структуре зависимости от Ширины с различают высокоомные (Z я;50 Ом) диэлектрика -экран. Как будет показано, наличие поверх-

низкоомные (Z, <50 Ом) линии. В первом приближении излучение стных волн прн определенных параметрах подложки может при-щелей считается независимым. При более точном решении учиты- существенному снижению излучающей способности полос-

вают их взаимную связь по внешнему пространству Входное со ковых антенн, когда значительная часть подводимой мощности противление определяют трансформацией сопротивления щелей i У^ затрачиваться на возбуждение паразитных поверхностных точкам питания. Наличие диэлектрика учитывают введением для следует обратить внимание при конструировании

линий эффективной диэлектрической проницаемости подложки колосковых антенн, работающих в коротковолновой части санти-Данный метод позволяет приближенно оценить резонансную длин\ трового и миллиметрового диапазонов волн, полоскового излучателя и рассчитать его ДН как результат пзлу В последнее время получили развитие несколько новых мето-чения двухэлементной антенной решетки магнитных вибраторов позволяющих рассчитать характеристики излучения МПА с Дальнейшее развитие рассмотренного метода привело к матема- Учетом поверхностных волн. Один из них основан на решении тической модели полоскового излучателя в виде прямоугольного Уравнения Поклингтона относительно неизвестного распределения резонатора с магнитными стенками по его периметру [6, 25] (см. ка по антенне с использованием соответствующей функции Гри-гл. 3). , . . полученной для задачи возбуждения поля горизонтальным

В 50-е годы был предложен метод для анализа полосковых Диполем Герца на диэлектрической подложке [36-38]. Решение линий на основе модели, прн когорой линия передачи заменялась Роводится методом моментов. При интегрировании потенциалов эквивалентным волноводом с магнитными стенками (модель Оли возникают определенные сложности, связанные с вычислением нера) [1]. Ширина волновода Сэф и диэлектрическая проницаемость ч^ интегралов в полюсах. Число полюсов подынтегрального материала Бэф, заполняющего его внутреннее пространство вы Р^жения определяется числом возбуждаемых в структуре побирались из условия равенства характеристических сопротивле рхностных волн. Метод позволяет вычислить сопротивление НИИ и постоянных распространения полосковои линии и эквива лучения поверхностных волн с помощью теоремы о вычетах, 30 31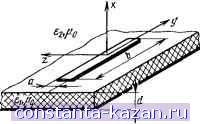

однако получить представление о диаграммах излучения при это^

не удалось. 2.2. ЛЕНТОЧНЫЙ МИКРОПОЛОСКОВЫЙ ВИБРАТОР

Несколько иным методом исследуется излучение линейно| МПА в [39]. Вначале записывается выражение для векторного по 2.2.1. Сопротивление излучения вибратора. Эффективность тенциала А горизонтального электрического диполя на подложк чения и простота выполнения схемы возбуждения ставит по-с использованием граничных условий для полей в плоскости ра, .,о(.овый вибратор на одно из первых мест по использованию при дела воздух -диэлектрик. Это выражение должно удовлетворят jjpcTpoeHHH малогабаритных антенных систем. Вибраторы приме-уравнению Гельмгольца, решение которого с использованием ии g качестве элементов микрополосковых антенных решеток тегралов Зоммерфельда позволяет определить компоненты А дл известно большое число конкретных модификаций микрополоско-двух областей (в подложке и воздухе). Наибольший интерес^ вибраторов (МПВ). однако для большинства из них излу-представляет компонента вектора напряженности магнитного по jjjj элементом является от-ля, перпендикулярная плоскости раздела сред. Условие равенств. 3 открытой микрополосковой

€е нулю на поверхности проводящей полоски используется в лалъ (МПЛ) ленточный ви-

яейшем для нахождения распределения возбуждающего тока igpa.i,op

определения резонансной частоты антенны [40]. Проанализируем более под-

Из рассмотренных методов расчета характеристик полосковыПробно электрические характери-антенн более точные решения дают вариационные методы, котостики ленточного вибратора, ко-рые используют выражения функции Грина, определяемые дл торый может рассматриваться горизонтального диполя Герца на диэлектрической подложке кaк модельная конструкция для проводящим экраном. Таким образом, в этом случае помимо со многих разновидностей МПВ. Непротивления излучения, обусловленного пространственными bo.i которые способы возбуждения нами, удается рассчитать и сопротивление, обусловленное возбуж вибраторов будут рассмотрены в даемымп в структуре поверхностными волнами. Однако наличп1§ 2.3 (см., например, рис. 2.17). полюсов в подынтегральном выражении, вызванное существова Рассмотрим излучение,МПВ (рис. 2.1) в виде отрезка МПЛ нием этих волн, существенно усложняет решение задачи определс длиной Ь, шириной а, расположенного на слое экранированного ния параметров МПА. Использованное представление функцн! диэлектрика (толщина слоя d, диэлектрическая проницаемость Грина соответствует разложению электромагнитного поля по bo.i материала е,). Найдем решение поставленной задачи в предполо-нам типов Е, Н относительно оси, перпендикулярной плоскост! женин заданного линейного тока на вибраторе: раздела сред (см. § 1.3). Такое представление не дает полно!

информации об излучательной способности пспосковых антенн J (у) = (у)/<2 = cos (ру/6)/а, (2.1)

так как не позволяет рассчитать ДН поверхностных волн. Знанп1

последних необходимо при построении антенных решеток для мп где а^ -единичный вектор; р - постоянная распространения ква-нимизации влияния полосковых излучающих элементов друг Исзи-Т волны в МПЛ, отрезок которой образует МПВ друга И на питающие их линии. Кроме того, при таком подход п., /01ч

достаточно сложно рассчитать зависимости сопротивления, oб^ , рассматривать как первое приближс-

словленного поверхностными волнами, а также и другие характ! поверхности боа истинное распределение тока на

ристики, в которые оно входит, от параметров подложки и геомет 1°

рическнх размеров антенны Исследование МПВ начнем с определения полного сопротив-

От приведенных недостатков свободно представление Функщп f характеристика при заданном токе (2.1) может Грина в виде разложения по волнам типов LE, LM. В этом случж^япм П'п м' указывалось в § 1.5, несколькими методами: подынтегральные выражения не имеют особенностей и задача мс BaSnl !. сопротивление в прямых

жет быть легко подготовлена для численного решения на ЭВА1л\ я ГД Р реакция [51]-как

Данное предоставление позволяет достаточно просто записать вь. Е^оГдеин эт V электрического

ражения для ДН волн, связанных с диэлектриком (поверхнос! t

Рис 2.1 Микрополосковый вибратор

ных) и излучаемых в открытое пространство. Существенно упро щается также расчет частотных и геометрических зависимосте! параметров МПА. Тензоры Грина в виде разложений по волнам типов Е, Н и LE, LH для нескольких видов областей со слоисты диэлектриком приведены в § 1.3, 1.4.

= 11/(У)Г„;,у(х^х' = 0; у, у'; z. z)J{y) dS dS.

(2.2)

Выбрав разложение функции Грина по волнам LE, LM, мож- 0 выписать непосредственно из (1.24) компоненту >~П57