- те V

-{-klW(p)W*(p)dg(z, z)ldzdz\d%d-n. (2.3

Первое слагаемое в (2.3) имеет дискретный спектр и соотвег ствует конечному числу поверхностных волн, возбуждаемых npi заданных значениях d и ei, а второе - непрерывный спектр и со ответствует пространственной части поля.

Воспользовавшись аналитической записью собственных функ ции Л! и Ч' и выполнив интегрирование в (2.3) по поверхност, вибратора, получим сопротивление излучения

2*) и сферической (для системам координат, получаем формулы для вычисления активных чисел сопротивления МПВ:

= 60 2 V (Kly j . Ф) <os 2 Ф dФ, (2.8)

V о

/?л = 60 2 V (v) J к. Ф) sin Ф Ф, (2.9)

Z = Z + Z5 + r,

(2.4

-v/g [1+ -)]оИ-У (2-

Z =i-i/Kffr (!!!!!lL L4-

1 1 - exp(-yta)

(та)2

2 4-(e;ctgM)4 В' ()

dcdr,.

Здесь

T = l/A:g-S-V . 2А:2 А:2 + 2, е; = е.,Ч,

Д (Т) -г В ~

(P-)s..n(?*/2)

/Gf- (0--)2

Y-.ft = ftoVl+(aJ.)2 r,2,

А*. -нормы собственных функций Xv, t, <*-корни систе мы трансцендентных уравнений (см. § 1.4, случай 2).

Выделив в (2.4) - (2.6) вещественную часть и перейдя в пр странстве волновых чисел от декартовой к цилиндрической (дл

Iisln*esin2<p cos*?

120 р Д2(е,у)

~1Г J j 1 - sin 2 0 cos2<p Ll? + (el Sine COS -f ctgl,M)

(sin e COS 6 cos y)

(sinecos<p)2 4-(£,ctgMo< J

sinededcp.

+ (2.10)

где

= Уе\ - 1 (sin b cos <p)2.

cos {0,5kob sin Ф l/l+(a:- ))- cos(0,5pf;)

(P-*?Kl+K-T)sin(0,5p6) sin (OMod cos Ф VTTK)

O.SAioa cosФl/l+ )2

(2.11)

£/0 \ B cos (O.Sfep sin e sin y) - cos (0.5) sin (0,5оа cos 6) [p2 (A sine sin )2 sin (0,56) O.Sftjacose

Множители типа sinx/x, содержащиеся в (2.11) - (2.12), есть результат интегрирования постоянного распределения тока поперек вибратора (координата х). При учете особенности на краях полоски функции типа sinx/x следует заменить на /о(х)-функцию Бесселя нулевого порядка. Для узких вибраторов {кф1) при вычислении активных частей сопротивления эти множители принимаются равными единице. Для узких полуволновых МПВ {Ь=0,5ко) выражения (2.11) -(2 12) упрощаются. Например, дли множителя пространственной части сопротивления

fife \ 2 cos (0,5u sin 6 sin ср) 1 - (sinesln9)2

Аналогично выражениям (2.8)-(2.10) могут быть записаны реактивные части сопротивлений X.

Основным методом анализа полученных выражений является проведение численных расчетов на ЭВМ. Упрощению алгоритмизации задачи способствует отсутствие в формулах типа (2.4) - (2.6) особых точек, свойственных решению граничных задач для слоистых сред при использовании стандартных представлений Функции Грина.

3* 35

Результаты расчета сопротивления полуволнового МПВ от толщины подложки для двух значений относительной диэлектрической проницаемости е[ даны на рис. 2.2. Здесь же приведен проверочный график сопротпв-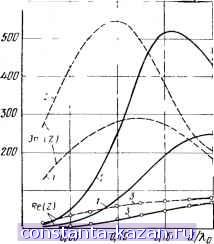

ления излучения плоского вибратора над экраном в отсутствие диэлектрического покрытия, на котором точками отмечены значения, найденные методом интегрального уравнения. Из указанного сравнения видно, что задание тока в первом приближении (2.2) во многих случаях позволяет находить значение сопротивления излучения, а вместе с ним и целый ряд других характеристик МПВ с достаточной точностью. Однако при определении некоторых параметров (например, резонансной длины вибратора) требуется более высокая точность вычислений, которая достигается при учете, помимо основной, пробных функций высшего порядка, аппроксимирующих истинное распределение тока. 2.2.2. Распределение тока по вибратору. Пусть линейный полосковый вибратор возбуждается в точке г/о напряжением V. Под действием стороннего напряжения на поверхности металлической полосы установится ток

J(a:. у) = /(у)/(.*:)а,.

Функции 1{у) и должны удовлетворять граничным усло-

виям на контуре вибраторов. Для узких полос (a<fc, а<Х) часто полагается /(jc) = l. Квазистатическое решение для металлическоп полосы шириной а приводит к следующему представлению /(л;), которое удовлетворяет условиям на ребре [1, 28]:

/(х) = (2/.).[1- (2<а)М->2.

Для упрощения последующих выкладок положим /(-*:) = 1 и учтем квазистатическую поправку в конечном результате.

Неизвестная функция определяется решением интегрального уравнения

fr : (-.y; \y)JW)dSV,b{y-yX (2.131

Рнс. 2 2 Зависимость сопротивления МПВ от параметров диэлектрической подложки:

/ е',=2,4; 2 -е', = 3,5; 5 -ei = l; а=0,028ло, 6 = 0,5?vo

которое непосредственно следует нз удовлетворения граничным условиям для напряженностн электрического поля на поверхности вибратора.

Вследствие сложности ядра уравнения (2.13) целесообразно для его решения использовать один из прямых вариационных методов, например метод Галеркнна. В соответствии с этим методом неизвестная функция раскладывается в ряд по функциям некоторого базиса фр {tj):

y(y) = l/a.2 fp(y). (2.14)

Подстановка (2.14) в (2.13), умножение правой и левой частей уравнения на одну из пробных функций 9(1/) и интегрирование по поверхности вибратора приводят к следующей системе линейных алгебраических уравнений:

i;pp.= iw 9=1.2,..., р р=1

или в матричной форме

[pJl/p] = Vo[ ], (2.15)

где [л]-столбец возбуждающих элементов, члены которого рассчитываются по формуле

, = 1/а-[<рЛу)8(у-Уо)йГ5.

Элементы квадратной матрицы Z имеют физический смысл взаимных сопротивлений совмещенных вибраторов с распределением токов -Рр(у), 9 (у). При р = 9=1 имеем сопротивление антенны Z , записанное в (2.2) при заданном токе. Активная н реактивная части сопротивлений вычисляются по формулам, аналогичным (2.8) -(2.10) с заменой выражений для В в (2.11) на выражение, вычисленное по формуле

= 11 (у) fp (у') ехр \-}% {X - х') - jr (У - у')\ dSdS.

Ток на входных клеммах антенны

/о= \J{y)b(y-y,)dS\\a. 2 \h%{y)4y~y,)dS Л

или в матричной форме /о = [я]< [/р], где [ ], -матрица-строка.

Умножив правую и левую части уравнения (2.15) на матрицу, обратную [Zp,]-[ZpJ-, получим выражение [/р| = Vo [р,]-( Ь которое после умножения слева на матрицу [п], приводит к формуле для входного сопротивления антенны:

1 Ь\1Л = /о = \п\ ]ZpJ-> ( ]. 1/Z, = /,/1, = \п\, [Zp,]- [п]. (2.16)

Искомое распределение тока на вибраторе также связано с обратной матрицей сопротивлений:

/(y) = n/ -[?{y)b[J- [ ]

Сделаем несколько замечаний по поводу выбора системы пробных функций (fp(y), так как их удачный выбор влияет на быстроту сходимости решения.

Прп возбужденнн МПВ в центре (уо = 0) распределение тока является симметричным, поэтому в качестве базисных могут быть выбраны следующие тригонометрические функции:

(у) = cos [{2р - 1) р=1,2, ...

При таком выборе матрица свободных членов превращается в единичную - [ ]=[£] и запись для входного сопротивления антенны принимает вид

р=1 9=1

Представляет интерес также такая система базисных функций, при которой учет высших членов ряда записывается как аддитивная добавка к решению задачи в первом приближении (например, к Zii в случае входного сопротивления). Этому условию удовлетворяет система функций

9i iVo) = . fp О') = sin (i-.ply] lb), fp (уо) = 0, p = 2,4, ...

Систему уравнений (2.15) перепишем в следующем виде: первое уравнение - в неизменном виде, а последующие - в виде, преобразованном таким образом, что в столбец свободных членов вынесены сопротивления, связанные с током первой гармоники:

I,Zp=I,Z + 2fp,.= Vo,

р-1 р=2

Для резонансных антенн второе слагаемое незначительно и может рассматриваться как поправка к решению задачи в первом приближении.

Параллельно со случаем сосредоточенного возбуждения МПВ напряжением Vo представляет практический интерес его возбуждение от линии питания с характеристическим сопротивлением Z и .напряжением падающей волны (Упад. В этом случае вместо уравнений (2.17) имеем:

Л^п + [Р1 ЬКр1 = 2/пад - Л^с Из второго уравнения и после подстановки в первое последовательно имеем

AZ - Л [z [, [z-j- [z,p] = 2(; з. -

откуда следует искомое распределение тока на вибраторе

Лу) = , {V. (у) - (у)Ь [ZJ- [рг]}-a[Z + Z)

Множитель 2UmRl(Zo-\-Zc) может быть преобразован следующим образом:

Z, Zo + z.

= /naa{l-[l-2Z,/(Zo+Z,)]} = /n,Jl-r],

где Г= (Zq-Z )/(Zo-f-Z)-коэффициент отражения в линии питания; /пад -ток падающей волны. Для входного сопротивления остается справедливой формула (2.18).

На рис. 2.3 показано распределение активной и реактивной частей тока вдоль МПВ длиной Ь = 0,5ло и шириной а = 0,5-10-Ло

(2.17)

или в матричной форме

AZ -f [z b[/p] = n. \z\,\\h\-i. [z,p].

Штрих у матрицы [Z] означает, что ее порядок уменьшен на единицу за счет вычеркивания первой строки и первого столбца.

Выделив из первого уравнения (2.17) [7] и подставив его во второе, получим входное сопротивление антенны

Zo = Volh =Z -[Z ]az;j- [Zg. (2.18)

10

Рнс. 2 3 Раснределеиие тока вдоль МПВ:

в) d=0,l/.o, ei=l,0, б) d=0,127?.o. е',=3,25; в) d=0,15o. е',=8,5