хан'ия в полосе пропускания резкому искажению характеристик на границах полосы запирания.

В § 3.08 изла,гались методы расчета оконечных звеньев, которые существенно уменьшают отражения в фильтрах, рассчитанных по характеристическим параметрам. Однако эти методы не дают возможности точно определить, какие максимальные потери на отражение будут в полосе пропускания. Таким образом, хотя метод характеристических параметров сравнительно прост, он требует большого практического навыка и связан с длительным процессом подстройки. Это существенно, если фильтр должен работать с малыми потерями на отражение и в строго заданной полосе. Расчет фильтров по рабочим параметрам обычно начинается с задания функции передачи, например, коэффициента передачи t, определяемого выражением (2.10.6) как функции комплексной частоты р. Затем по передаточной функции находится входное сопротивление цепи, опять в виде функции от р. После этого с помощью различных разложений функции входного сопротивления в цепные или элементарные дроби определяются элементы цепи. Полученная таким образом цепь будет иметь передаточную функцию, заданную в начале расчета, и тем самым исключается какая бы то ни было неопределенность и необходимость в экспериментальной подгонке. Характеристические параметры в этих методах расчета не используются, а влияние нагрузок учитывается в самом начале при задании функции передачи.

Вообще говоря, одни и те же фильтры нижних частот, рассчитанные по характеристическим и по рабочим параметрам, совер-шевно одинаковы по своей структуре. Однако для обеспечения заданной характеристики значения элементов фильтра, рассчитанного по рабочим параметрам, будут несколько отличаться.

При проектировании фильтров очень часто используются чебышевская и максимально плоская функция передачи. Они рассматриваются в § 4.03, где приведены характеристики фильтров; величины их элементов протабулированы в § 4.05.

При проектировании свч фильтров с помощью фильтров-1ирото-типов нижних частот на сосредоточенных параметрах приходится вводить некоторые приближения. Несмотря на это, метод обеспечивает достаточно хорошую точность расчета в пределах значительной части частотного диапазона. Вместе с тем он исключает элемент предположительности, присущий классическому методу расчета по характеристическим параметрам.

4.03. Максимально шоская н чебышевская харакгерисгнкн гатухания

На рис. 4.03.1 показана типичная максимально плоская характеристика затухания фильтра нижних частот). Частота eoj, соот-

*) Эта характеристика также известна под названием характеристики Баг-терворта.

- 78 -

ветствующая затуханию Lat, назы-вается праничной частотой полосы пропускания (илн частотой среза фильтра). Максимально плоская характеристика описьевается следующим матемагическим выражением): ,

Л ( .) = lOIg

, дб, (4.03.1)

antilg-if -1.

(4.03.2)

Рис. 4.03.1. Мжсимал^ плоская характеристика затухания

Такую характеристику можно получить с помощью фильтров нижних частот (см. §§ 4.04 и 4.05). Параметр п в выражении (4.03.1) равен числу реактивных элементов цепи. Эта характеристика получила название максимально плоской в связи с тем, что все производные до (2п-1)-го порядка включительно от величины, которая заключена в выражении (4.03.1) в квадратные скобки, равны нулю при и' = 0.

В большинстве случаев частота среза toj для фильтров с максимально плоской характеристикой определяется как частота, соответствующая уровню затухания 3 дб. На рнс. 4.03.2 приведены характеристики затухания в полосе запирания фильтров с максимально плоской характеристикой прн различном числе элементов 1-15 и Еа,=Ъ дб. Для удобства пользования на графике по оси абсцисс отложена величина to7<Oi. - 1- Использование знака абсолютной величины обусловлено тем, что при переходе от фильтра нижних частот к полоснопропускающему или полоснозапираю-щему фильтру отношение a,lvy\ может принимать отрицательные значения, которым будет соответствовать такое же затухание, как и для положительных значений

На рис. 4.03.3 приведена другая очень распространевиая характеристика, которая получила название чебышевской или равно пульсирующей. Здесь Lat так же, как и в предыдущем случае, является максимальным затуханием в полосе пропускания, а oj -

*) Редко встречающийся в русской технической литературе символ antilg обозначает функцию, обратную логарифму (десятичному) и определяемую сле-дуюиим образом: если a=lgb, то *-.antilga=10 . В практических расчетах при пользовании таблицами десятичных логарифмов понятие обратной логарифмической функции дает определенные удобства, поэтому здесь и далее в книге сохранены это понятие и соответствующий символ antilg. принятые в оригинале {прим. ред).

- 79 -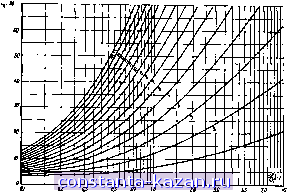

Рис. 4.Ш.2. Максимально плоские характеристики эату-хания. Граничная частота oi соответствует уровню 3 аб

граничной частотой. Чебышевская характеристика затухания описывается следующими математическими выражениями:

Z.H(o)=10lg

i( o) = 10lg

I при (4.03.3)

при а а[, (4.03.4)

Рнс. 4.03.3. ЧебышЕЕокая характеристика затухания

1 + г cos п arccos ( 1+Ech У Arch -j

e = [antilg

Этот тип характеристик также может быть получен с помощью структур фильтров, рассматриваемых в §§ 4.04 н 4.05. Параметр п в выражениях (4.03.3) и (4.03.4), как .и в случае максимально плоской характеристики, равен числу реактивных элементов цепи. При п четном имеется п/2 частот, на которых для чебышевской характеристики, аппроксимирующей передаточную функцию фильтра нижних частот, Лл = 0. Прип нечетном бу-

Рис. 4.03.4а.

Чебышевские

\о т взв т to to w 7Sy характеристики затухания с пульсацнилиИ)-01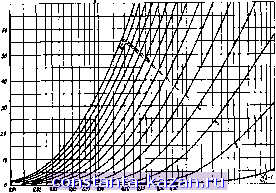

Рис. 4.03.46. Чебышевские характеристики затухания с нульсациями 0,1036 - 81 -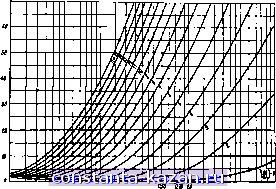

п ш KB № т т т ая

и а я не ю

Рис. 4.03.4в. Чебышевские характеристики затуханкя с пульсациями 00 дб

Ш Щ SIS OBJ

а т w oje Ф и se а w а

Рис. 4.03.4г. Чебышевские характеристики затухания с пульсациями 0,.50 5б - 82 -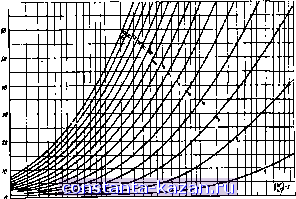

Рис. 4.03.4а Чебын1евские характеристики затухания с пульсациями 1,0066

т mm т т оя т ах т т ю е.о и ло и

Рис. 4.03.4е. Чебышевские характеристики затухания с пульсациями 2,00 об