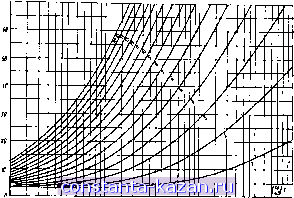т т вв 07 аи 02 вя вя ш т z as и zj Рис. 4.03.4аг. Чебышевские характеристики затухания с пульсациями 3,00 56

дет (;i+l)/2 таких частот. На рис. 4.03.4 приведены характеристики затухания в полосе запирания для чебышевских фильтров с максимальным затуханием в полосе пропускания Лаг=0,01; 0,10; 0,20; 0,50; 1,00; 2,000 н 3,000 дб. На оси абсцисс, как я ранее, отложено т7ш, -1.

Интефесно сравнить максимально плоские характеристики затухания на .рис. 4.03.2 с чебы.шевскнми характеристиками на рис. 4.03.4. Из графиков видно, что для одного и того же максимального затухания в полосе пропускания и при одинаковом числе реактивных элементов хараитеристика затухания в полосе за-п[1рания чебышевского фильтра имеет ббльшуку крутизну. Например, максимально плоская характеристика на рис. 4.03.2 и чебышевская иа рис.4.03.4ж имеют одинаковое максимальное затухание i.Ar=3 дб, но при л=15 затухание 70 дб для максимально плоской xaipaKTepHCTHKH достигается при m=l,7mj, тогда как для чебышевской - уже при eo=l;18coJ. Поэтому с точки зрения крутизны характеристики чебышевские фильтры предпочтительнее. Однако при наличии значительных диссипативных потерь в реактивных элементах форма характеристики в полосе пропускания обоих типов фильтров изменяется, причем в случае чебышевского фильтра эти изменения проявляются резче. Вопросы влияния потерь на форму характеристики будут рассмотрены в § 4.13. Обыч-- 84 -

но считают, что фильтры с максимально плоскими характеристиками вносят меньшие фазовые искажения, чем чебышевские фильтры. Однако в § 4.08 будет показано, что это не всегда справедливо и зависит от величины Lat.

Максимально плоская и чебышевская характеристики, приведенные на рис. 4.03.1 и 4.03.3, те являются единственно возможными характеристиками такого типа. Например, чебышевские характеристики согласующих цапей, рассматриваемых в §§ 4.09 и 4.10, имеют ту же форму, но минимумы равяошульсирующей кривой затухания при этом не равны нулю. Иногда чебышевские фильтры рассчитываются таким образом, чтобы иметь равнопуль-сирующее затухание как в полосе пропускания, так и в полосе запирания. Фильтры с такими характеристиками довольно широко используются в низкочастотном диапазоне, однако их трудно точно рассчгптать для использования в овч диапазоне. Одним из возможных исключений является свч фильтр, рассматриваемый в § 7.03.

4.04. Определение парашетров фильтров-прототипов нижних частот

Б этой главе обозначения go, gi, g2, .-, gn, gn+i для элементов фильтров-прототипов нижних частот приняты в соответствии с рис. 4.04.1. Один из возможных вариантов фильтра-прототипа по-

Рис. 4.04.1. .К определению элементов фильтра-прототипа

казан на рис. 4.04.1с, а на рис. 4.04.16 приведена его дуальная схема. При расчете может быть использована любая из схем, так как их характеристики идентичны. В связи с тем, что схемы представляют собой взаимные цепи, любое из активных сопротивлений как на левом, так и на правом конце можно рассматривать как внутреннее сопротивление генератора. Следует отметить, что обозначения на р.ис- 4.04.1 имеют следующий смысл:

индуктивность последовательной катушки и.ти емкость параллельного конденсатора; 85 -

сопротивление генератора К', если gi=CJ, или проводимость генератора Gj, если g]=L[;

сопротивление нагрузки если gn=C, или про-

водимость нагрузки G.ji, если g = L.

Причиной выбора таких обозначений является то, что при нх использовании уравнения получаются одинаковыми как для схемы на рис. 4.04..1Я, так п для дуальной ей схемы. Кроме элементов gh, S прототипе используется параметр ш,. Он является граничной частотой полосы пропускания и для рассматриваемых здесь максимально плоских и чебышевских фтьтров показан на рис. 4.03.1 и 4.03.3. Определение этого параметра для фильтров с максимально плоской характеристикой времени задержки дается в § 4.07.

Величины элементов прототипов, рассматриваемых в данной главе, нормируются так, чтобы go=l и Ш[ = 1. Переход от нормированных фильтров-прототипов .к другому уровню сопротивлений и измененной шкале частот легко осуществляется с помощью следующих преобразований элементов цепи:

для активных сопротивлений или проводимостей'

для индуктивностей

(4.04.2)

(4.04.3)

л для емкостей

В этих формулах величины со штрихами относятся к нормированному .прототипу, а без штриха - к преобразованной (ренормиро-ванной) цепи. Как было сказано выше, для прототипов, рассмат-рийремых в данной главе, go=Sb=l или go=U=i. Чтобы показать, как выполняется это преобразование, приведем следующий пример.

Имеется фильтр-шрототиц нижна1х частот с элементами Я' - = 1,000 оы; С, = 0,8430 ф; Ц =0,6220 гн и =1,3554 мо. Значения элементов соответствуют чебышевскому ф.ильтру с величиной пульсаций 0.10 дб и граничной частотой полосы пропускания <oj =1 рад (см. табл. 4.05.2 при. /1=2 и пульсации 0,10 дб). Требуется найти значения элементов фильтра нижних частот, нагруженного на чисто активное сопротивление i?o=50 о.м с граничной частотой полосы пропускания /i = 1000 Мгц.

-86-

Находим {Ro/R-=50 н (ш,/ш.) =1,/2я-10 =0,159-10- . Далее с помощью соотношений (4.04.2) -(4.04.4) получаем:

Ло = 50 ом; Ci = --0,159-10- -0,8430 = 2,68-10 -= ф; 50

Z. = 50-0,159-10~° 0,6220 = 4,94-10 гн;

Сз = -. 1,3554 = 0,0271 JKO. 50

4.05. Фильтры-прототипы с максимально плоской и чебьппев-ской характеристиками, нагруженные с двух сторон

Величины элементов максимально плоских фильтров, нагруженных на активные сопротивления на входе и выходе я имеющих Аг=3 дб, go=l и т;=1, могут быть найдены из следующих выражений [5]:

go=U

g,= 2sm

{2к-1)п

2п

. А = 1,2,

(4.05.1)

= 1.

В табл. 4.05.1 приведены значения элементов таких фильтров, содержащих от ;i=.l до п=15 реактивных элементов.

Для чебышевских фильтров, нагруженных с двух сторон и имеющих характеристики вида рис. 4.03.3 при условии, что go=l и <й , =1, а 1аг задано в децибелах, величины элементов могут быть рассчитаны следующим образом [4, 5]. Сначаша определяются вспомогательные параметры по формулам:

p = ln(cthif,); 1=sh;

(4.05.2)

Затем находятся величины элементов:

8 +\ =

1, если п нечетное; cth(p/4), если п четное. - 87 -

в табл. 4.05.2 приводятся величины элементов для таких фильтров, соответствующие различным значениям Lr и с числом реактивных элементов от п=1 до п=.15.

Следует отметить, что все прототипы, рассматриваемые в данное! параграфе, будут симметричными при нечетном п. Бели п - четное, то они обладают свойством антиметрии, о котором упоминалось в §§ 2.11 и 3.07. П|ри этом условии одна половина цеои является обратной по отношению к другой ее половине с точно- стью до положите-чьного вещественного множителя Кл, определяемого соотношением

Rn=[RoRn+i , (4.05.3)

где и Ri, - сопротивления нагрузок на в.ходе и выходе. Если - сапротивление одной из ветвей фильтра лестничного типа, то

(4.05.4)

где Z i s - сопротивление дуальной ветви на другом конце фильтра. Из равенства (4.05.4) видно, что индуктивные сопротивления на одиом конце фильтра связаны с емкостными проводи, мостями на другом конце соотношеянем

01 Lb

(4.05.5)

Т0.4Н0 так же

o>n+i-k = R>C;. (4.05.6)

Пользуясь приведенными соотношениями, можно иайти величины элементов второй половины антиметричного фпльтра из элементов первой половины (это можно сделать также и в случае симметричного фильтра).

Л1агксимально плоские и чебышевские фильтры, нагруженные с двух сторон и имеющие структуру, показанную на рис. 4.04.1, будут обладать рассмотреаиымн выше свойствами симметрии и ант11.метрин только в том случае, если La -О на одной илн нескольких частотах в полосе пропускания (как ва рис. 4.03.1 и 4 03.3). Фильтры с чебышевскими пли максимально плоскими характеристиками, рассматриваемые в §§ 4.06, 4,09 и 4.10, не обладают этими свойствами. Фильтры с максимально плоской характеристикой времени задержки, которые рассматриваются в §4.07, не являются ни си.мметрнчкыми, ни антиметричными, даже если La=0 на частоте ш'=0.

В некоторых редких случаях могут потребоваться прототипы с числом элементов н больше 15. .Хорошим приближением в таких случаях явится расчет, при котором у прототипа с н=14 пли IS