На DHC 4 06 le приведена схема, дуальная предыдущей. Здесь цепь возбужд*гся идеальным генератором тока и поэтому нсполь-зуется функция ослабления по току:

li = 20lg

= 101g

, дб.

(4.06.5)

где и II. ?оИ 2: определены па рисунке. Если Lam Ur в § 4.03 заменить соответственно величинами и или L, и Ur. то все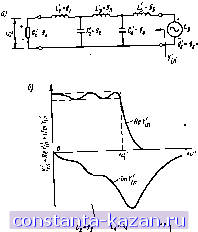

Рис 406.1. Пятизлеыетпый фильтр, и=-Р5 5 нойстороны- а-иема с идеальным генератором напря- еии™б-примерный характеристики В-СД Р-этой схемы; в-дуальная схема

водимости У; для

с идеальным генератором тока

Г кксим1льно плоской характеристиками, нагруженными с одной стороны.

Из выражения (4.06.1) следует, что при данном генераторе напряжения Eg передаваемая мощность полностью определяется вещественной частью входной .проводимости Re5j . Таким образом, для того чтобы ф|Ш1ьтр имел максимально плоскую нли чебышев-скую характеристику, необходимо, чтобы проводимость Re У' также аппроксимировалась той же самой характеристикой. На рис. 4.06.1Й показана приблизительная форма характеристик ReV; \тУ для цепн на рнс. 4.06.ila в случае, когда она имеет чебышевскую характеристику передачи.

Как будет показано в гл. 16, отмеченное свойство вещественной части входной проводимости или сопротивления (т. е. Re У' или Re Z ) для фильтров, нагруженных с одной стороны, делает их очень полезным при проектировании диплексеров и мультиплек-серов. Кроне того, подобные шрототипы могут использоваться при расчете фильтров, возбуждаемых генераторами, характеристики которых приближаются к характеристикам идеальных генераторов напряжения или тока. HaimpHMep, пентод в анодной цепи можно представить в виде генератора тока с параллельно включенной емкостью. Такая схема может быть широкополосной только при условии, что параллельная емкость будет использована в качестве первого элемента фильтра, нагруженного с одного конца.

Орчард (Orchard) [5] вывел формулы для фильтров с максимально плоской характеристикой, нагруженных с одной стороны и нормированных так, что граничная частота wj = 1 соответствует уровню 3 дб (т. е. L,=L,r илн Le=Ls, равно 3 дб) и gD=l. Эти формулы могут быть записаны в следующем виде;

л (ai -1)

а значения элементов .равны:

, 4=1,2, 1, 2, . . .,

(4.06.6)

a = <Ji;

, * = 2, 3.....n;

= co

(проверка: gn=ngi).

Величины gh в этих формулах определяются в соответствии с рис. 4.04.1а и б. В табл. 4.06.1 приведены значения элементов таких фильтров для п=1-\0.

Для фильтров с чебышевской характеристикой, нагруженных с одной стороны, при условии, что go=\, ю, = 1, а величина пуль-

саций в полосе шропускания равна Z. нли Le йб, формулы Орчар-да [5] имеют вид:

1 нпк Lp

Р = 1п

cth-

17,37

о sin-iI<H=i)-.ft=l,2.....щ

d. = (Y=+sin=-)cos= . ft= 1. 2. .. ( - 1), (4.06.7)

а значения элементов .равны:

. ft = l, 2.....л;

В табл. 4.06.2 приведены значения элементов для чебышевскн.х фильтров, нагруженных на одном конце, прн различных пульсациях iB .полосе пропускания.

4.07. Прототипы фи.1п>тров с максималыю плоской характеристикой времени аадержки

Коэффициент ослабления по напряжению £j/£2 (см. § 2.10) для нормированного фильтра с макси-мальио плоской характеристикой времени задержки может быть определен выражением 19, 10]

~=с(р'Гу (\1р'),

(4.07.1)

где я=а'--1ю' -нормированная комплексная частотная переменная; с-вещественная положительная постоянная;

- полиномиальная функция Бесселя с аргументом 1/р'.

Используя урниие (4.07.2), можно привести выражение (4.07.il) к простой полиномиальной форме:

= Р (Р') = (Р> +(р') -а„ 1+ . . .-fpa,+flo. (4.07.3) 1 -99-

ЗНАЧЕНИЯ ЭЛЕМЕНТОВ ДЛЯ ФИЛЬТРОВ С ЧЕБЫШЕВСКОЙ ХАРАКТЕРИСТИКОЙ НАГРУЖЕННЫХ С одной СТОРОНЫ ПРИ УРОВНЯХ ПУЛЬСАЦИИ 0,l-i-3.0 дб

ТАБЛИЦА 4.06.2