- ci сч ci

s g g

E Й S i

- M (N CJ

g I g ffi Ю g Й

-* сч м ci ci ci ci ci

CC 35 QO -

Й s s s

t- OD jt C

я 2 S g S

Di ci ci ci

- 41) t- in

Cn о 41- CO t- Ю

i 2 s К s iq IS

w <N ci ci im eg

in >n -ч- о - - m - О) rt so

Й S S S ft й

S S 2 g

t-, GO СП Ol

ci ci ci СЧ ci ci ci сч

S о *ff>

Ё Г- * (2 t£ S

- IM rt >Л CD

Если положить

ф = arg -

= Arctg----- , рад.

(4.07.4)

то в соответствии с § 1.05 время задержки (т. е. групповая задержка) равно

(4.07.5)

где и' - круговая частота в рад/сек.

Передаточная функция, определяемая выражениями (4.07.1) и (4.07.2), обладает тем свойством, что соответствующая ей групповая задержка имеет максимально возможное число производных по частоте ш', обращающихся в нуль в точке и>=0. Именно поэтому в данном случае говорят, что цепь имеет максимально плоскую характеристику времени задержки. Время задержки может быть выражено следующим соотношением [9, 10];

(4.07.6)

- функции Бесселя от аргумента ш7т[ и

- грушповая задержка при ш'-й). .Модуль функции fj/fij равен

\ -1-

(4.07.7)

(4.07.8)

и с увеличением п затухание приближается к гауссовой форме 19, 10, 11]:

со у

(2п-1)1п10

(4.07.9)

Для п^З ширина полосы на уровне 3 дб приблизительно равна

(] =/(2п-1)1п2. (4.07.10)

\ 1 /ЭТИ)

Вейиберг [9] составил таблицы величин элементов для нормированных фильтров с максимально плоской характеристикой времени задержки. Значения элементов в табл. 4.07.1 взяты из его - 103 -

eS II

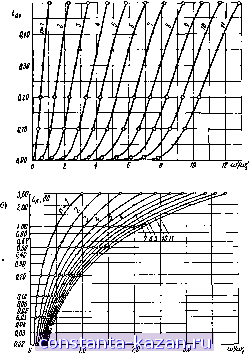Рис. 4.07.1. Время задержки fa) и затухание в полосе про-я пускания (б) 11.1я фильтров с максимально плоской харак-

теристикой времени задержки

работы. Нормировка прошзведена так, что <5 = 1/к1, = 1 сек, а go=l- Чтобы получить желаемое время задержки Ido, отличное от еобходимо изменить частоту в соответствии с отношением

(4.07.11)

а затем преобразовать величины элементов цепи согласно методике, изложенной в § 4.04. Вейибергом также опубликованы результаты вьнисления временной задержки и Затухания в окрестности П0.10СЫ пропускания для фильтров f: числом элементов =1-11. Этн результаты представлены графически на рис. 4.07.1 (кривые построены с помощью интернолировання между расчетными точками). Хотя у таких фильтров характеристики времени задержки в полосе пропускания почти постоянны (время задержки меняется очень незначительно), их характеристики затухания, как будет показано ниже, оказываются в общем случае хуже, чем у обычных максимально плоских нли чебыше-вских фильтров с тем же числом реактивных элементов.

4.08. Сравнение характеристик времени задержки различных фильтров-прототипов)

Если нагрузки фильтра-ч1рототипа равны или отличаются незначительно, то групповое время задержки при ю'->-0 можно вычислить из выражения

gn-элементы

(4.08.1)

.прототипа, определенные на

где g gs, рис. 4.04.1.

iB табл. 4.13.11 и на рис. 4..13.2 приведены также значения коэффициента С„, вычисленные для максимально плоских в чебышевских фильтров-прототипов. В этом случае для определения времени задержки .можно использовать точное равенство

<i = C , сек. (4.08.2)

Если фильтр-прототип нижних частот преобразовать так, что граничная частота eoJ станет равной eoi, то в|)емя задержки изменится и будет равно

(4.08.3)

Для полоснопропускающего фильтра, рассчитанного из фильтра-прототипа нижних частот, время задержки на центральной часто-

) В § 6.15 будут рассмотрены характеристики времени aa/ijepMiai еще нескольких т>пов схелл.

=) Это выражение получено Коном (S. В. Cohn) и может быть выветено с немощью ур-ний (4.13.9)-<(4.13.11).

те полосы пропуокания (по крайней мере для узких полос) равно )

t.f, (4.08.4)

где <ui и №2-граничные частоты .полосы пропускания полоснопропускающего фильтра, соотвеТ|Ствующие граничной частоте прототипа (й[.

Чтобы определить время задержки иа других частотах, необходимо рассмотреть функции передачи. Для всех фильтров-прото-ТИ.ПОИ, рассматриваемых в этой главе, функция ослабления по напряжению £j/£2, определенная в § 2.10, может быть представлена с помощью полинома Рп(р') таким образом, что

где p=o-)-itt) -комплексная частотиая переменная.

Для прототипа с максимально плоской характеристикой затухания, состоящего из п реактивных элементов, в случае, копа

=1 и 1аг=3 дб (см. рис. 4.03.1), Рп{р') три п четном равняется

п(р') = сП[(рТ + 2C0S а при п нечетном

п(2п1- 1)

2п

(4.08.5)

(п-1)/2

Рп(р') = с(р+ 1) П [{рУ + (205 )Р' + 1

(4.08.6)

2п (4.08.7)

где с - вещественная постоянная

Для фильтров-ирототипов с чебышевской характеристикой, состоящих из п реактивных элементов, в случае, когда га, =4, а ве-.тнчина пульсаций равна Lat, дб (см. рис. 4.03.3), Рп[р') при четном п определяется выражением

P.ip: .) = с П{(рТ +[2xcos il(!]/-b..fsin -M m=l

И при п нечетном, когда п^З, Рп(р:х) = с(р- + х) П

Эта задержка приблизительна и близка и реальной только для фпльтра с сосредоточенными параметрами, состоящего нз цепочки последовательны\ и параллельных резонаторов. Если в фильтре используются отрезки линий пере дачи, то имеет место дополнительная задержка, обусловленная нонечиой физической дпиной фильтра.

\ п / п

,(4.08.8)