костп, и индуктивности, в эквивалентные схемы, содержащие тйлько индуктивности илн только емкости. Это может быть сделано с помощью идеальных инверторов, приведенных на рис. 4.12.1 Идеальный инвертор сопротивления ведет себя на всех часто-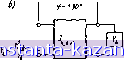

Рнс. 4.2.1. Идеальные инверторы сопротивления ffl) и проводимости (б)

та\. подобно четвертьволновому отрезку линии с волновым сопротивлением К. Поэтому, если он нагружен с одной стороны сопротивлением Zb, то сопротивление 2 со стороны других его зажимов б>дет равно

(4.12.1)

Аналогичное Представление справедливо и для идеального инвертора проводимости, если сопротивления заменить проводи-мостяин, I. е. он ведет себя на всех частотах подобно отрезку четвертьволновой линии с волновой проводимостью Таким об-разо.м, еслн инвертор на одном конце .нагружен на проводимость Уь, то проводимость Уа СО стороны других зажимов равна

i =- (4-12.2)

Как показано иа pi[c. 4.12.1, инвертор может иметь характеристический фазовый сдвиг <р, равный ±90° иЛИ нечетному нрагно-ыу этой -величины.

Вследствие преобразования, осуществляемого инвертором и вырах^енного в форме соотношений (4.12.1) н (4.12.2), последовательная индуктивность с (Инвертором на каждой стороне будет выглядеть как параллельная емкость, если смотреть со стороны внешних (по отношению к индуктивности) зажимов инвертора. Аналогично парал.-]слЫ|Яя емкость с инверторами на обеих сторонах- окажется последовательной индуктивностью, если смотреть со стороны внешнп.ч зажимов инвертора. Используя это свойство, можно преобразовать цепи-нротот][Пы иа рис. 4.04.1 в любую нз эквивалентных форм иа рис. 4.12.2. которые имеют характериств-ки передачи точно такие же, как у прототипов на рис. 4.04.1.

Каи следует из соотношений (4.12.1) и (4.1.2.2), инверторы обладают способностью изменять уровень сопротивлений или лро-Е0ДИМ0СТ6Й в зависимости от выбора значении параметров К - 132 -

im-j-

Рис. 4.122. Модиф|щпрованные прототипы нижних частот с инверторами;

сопротнвле НИИ (а)

ДО ni

проводимости (б)

Ч h+i

=1 до n-l

или }. По этой причине сопротивления Ra п Rk п индуктивности Lah на рис. 4.12.20 .- огут быть выбраны произвольно и характеристика будет идентична характеристике исходного прототипа- .на рис. 4.04.1 при условии, что параметры инверторов Кк.км определяются .по фор,- улам, указанным в подписи под рис. 4.12.2 для цепи а. То же самое справедливо и для цепи 6 только иа дуальной основе. С.тедует отметить, что величины gh являются величинами элементов прототипа, которые даны на рис. 4.04.1.

Теперь кратко рассмотрим получение выражений для Кк, я-н и 1к,к+\- Сопоставление прототипов иа рис. 4.04.1а и б с соответствующей цепью, иарример, на рис. 4.12.2а проводится с использованием понятия дуальности. Благодаря инвертору сопротивления данная цепь становится дуальной, если смотреть .иа нее со стороны входных зажимов инвертора (т. е. через него). Таким образом, входное сопротивление, которое мы видим со стороны катушки, toi на счеме рис. 4.12.2а, является точно таким же, как сопрогивление, которое будет видно со стороны индуктивности L[ - 133 -

на схеме 4.04.16 с точностью до постоянного множителя, характеризующего изменение уровня сопротивлений. Сопротивление со стороны катущки Lz на рис. 4.12.2а совпадает соответственно с сопротивлением, видимым от индуктивности L], Но ряс. 4.04.1 а, но опять с точностью до постоянного множителя. Рассуждая аналогично, можно показать, что сопротивление в любой точке цепи на рис. 4.12.2а может быть с точностью до постоянного множителя связано с соответствующим сопротивлением в депях а рнс. 4.04.1а и б.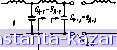

6) Ldi-I

Рнс. 4.12.3. К ВЫВОД) соотношений дтя параметров инверторов Kk,k+t

На рнс. 4.12.За показана часть прототипа нижних частот, разомкнутого непосредственно за емкостью Ck+i. Дуальная схема приведена на рис. 4.12.36, где прежний разрыв цепи стал коротким замыканием. Соответствующая цепь, использукидая только последовательные индуктивности и Л-ннвергоры, показана на рис. 4.12.3в. Все эти цепи удобно использовать при выводе выражений Kh,h+\ через toll, iiuii+i и значения элементов прототипа gn и gh+i- Разрыв цепи и короткое замыкание введены здесь только для упрощения уравнений.

Согласно схеме иа рис. 4.12.3а имеем

а для схемы на рис. 4.12.3s

(4.12.4)

тсгя LabiLk, характеризующего изменение уровня сопротивления. Поэтому

Z; = A=i.Z. ,-f ±. (4.12.5)

Приравнивая вторые члены в равенствах (4Л2.4) и (4.12.5), после некоторых преобразований получим

(4.12.6)

Так пак L;=gi, и Ci,+,gh+i, то выражение (4.12.6) эквивалентно выражению для Kh.h+i, приведенному в подписи под рпс. 4.12.2а. Очевидно, что если перемещать соответствующим образом положения точек, в которых цепь предполагается замкнутой или разомкнутой, то описанная выше методика может быть применена для расчета всех инверторов, за исключением оконечных. Следовательно, выражение (4.12.6) справедливо для А=1,2,..., п-1.

На рис. 4.12.4а показаны последние два элемента прототипа, а иа рпс. 4.12.4 6-соответствующая схема с К-инвертором.

Для цепи на рис. 4.12.4 а

а]----

а дтя цепи на рис. 4.12.46

Z =ia)Z. ,

Рис. 4.12.4. К выводу соотношений для оконечных инверторов

(4.12.7)

(4.12.8)

Гак как z; должно совпадать с Z с точностью до множителя Lan/L (масштабного коэффициента уровня сопротивлений), то

К= J-Zn=i>- + J-J-. (4.12.9

L о,

Прфзвнивая вторые члены выражений (4.12.8) и (4.12.9), полу-

(4.12.10)

Но Z должно совпадать с Z. с тоГностью до постоянного ножи- выражежГе f; :: пГи™еденное'в подпи™ pllc XiГ

- 135 -

Вывод формул для параметров /ь, s+i, приведенных там же, может быть выполнен аналогичным образом, если сопротивления заменить проводимостями (т. е. на дуальной основе).

4.13. Влияние диссипативных элепеитов в прототипах на фильтры нижних частот, полосыопропускающие и верхних частот

Элемеиты любого реального свч фильтра имеют конечную добротность Q, и во многих случаях необходимо знать, как она влияет иа затухание н полосе пропускания. Если фильтр рассчитывается из прототипа нижних частот, то конечную величину добротности его элементов удобно учесть введением в прототип диссипативных элементов н определением их влияния на характеристику прототипа/ Увеличение затухания в полосе пропускания прототипа, обусловленное диссипативными зле-чеитами, будет таким же, как и увеличение затухания в полосе пропускания (на соответствующих частотах) свч фильтра из-за конечной добротности его элементов.

Под добротностями элементов ), которые будут фигурировать в расчетных формулах, приводимых ниже, понимаются добротности элементов фильтров нижних частот на частоте среза (л определяемые выражениями:

(4.13.1)

Q.=° нли Q.= i, Rk

где Рк - паразитное сопротивление катушки (индуктивности Lk); Gk - паразитная проводимость конденсатора (емкости Ск) Ц. Если полосовой фильтр, рассчитанный из трототипа нижних частот, имеет ненагружеииую добротность ftiro резонатора в середине полосы пропускания, равную ((Jnne)b, то добротность Qk, соответствующая А-му реактивному элементу прототипа, равиа

(Эб=ш(<гппо)*. (4.13.2)

В этом уравнении w является относительной шириной полосы пропускания полосиопропускающего фильтра, причем ее граничные частогы соответствуют граничной частоте toj прототипа нижних частот (см. гл. 8). Ненагруженная добротность Q резонаторов

*) В данном случае понятии элемент и добротность элемента относятся к физичеоким элементам фильтра в виде катупжи индуктивности или конденсатора. Не следует путать определение понятия элемент, которое применено зде-ь. с используемым во всей книге понятием элемента цепи как идеализированного элемента типа /?, L или С, т. е. активного сопротивления, индуктивности или емкости (прим. ред.).

2) Здесь обозначения величии Ljt, Rk, С/я и использованные без штрихов, применимы к любому фильтру нижних частот иезавнсимо от того, является лн он нор.мнроваиньгм прототипом или иет. Дальше в этш1 параграфе в обозначения введены штрихи, чтобы отличить параметры прототипов нижних частот от параметров полоснопропускающих фильтров и фильтров верхних частот.

может быть вычислена с помощью данных, приведенных в гл. 5, или определена путем измерения, как показано в § 11.02.

В случае фильтра верхних частот, проектируемого на основе прототипа нижних частот, добротность элемента прототипа должна быть взята такой же, как и добротность соответствующего элемента фильтра верхних частот на его частоте среза.

Рий. 4.13.1. Фильтр-прототип нижних частот с диссипативными бле^чентамп

На рис. 4.I3.I показана часть прототипа нижних частот с введенными паразитными элементами, определяющими потери в схеме. Следует отметить, что паразитный диссипативный элемент, относящийся к реактивному элементу gk, обозначен через dbgk (введенный здесь параметр dk будет именоваться коэффициентом рассеяния). Используя это обозначение, можно написать ур- ие (4.13.1) в виде

г, let ш; to к

где ш, -граничная частота прототипа нижних частот. Таким образом.

1 С*

(4.13.3)

Тогда для лоследовательной ветви прототипа

Zk = iaLl+R ={iu> + di;jgi, (4.13.4) и для параллельной ветви

n-i q-fG;=(i(o-fd,)g,. (4.13.5)

Особый практический интерес представляет частный случай, когда добротности всех элементов одинаковы, т. е. dk=d для к от 1 до п. Из ур-ний (4.13.4) и (4.13.5) следует, что влияние рассеяния может быть учтено заменой частоты 1ш' для цепи без потерь комплексной частотой {un+d) для цепи с потерями. Например, эта замена можег быть сделана непосредственно в функциях передачи, т. е. в ф-пах (4.07.1) и (4.08.5)-(4.08.8) для того, чтобы рассчитадь характеристики передачи с учетом потерь. На постоянном токе функция iioi+d) равняется просто d, так что, еслн для - 137 -