прототипа без лотерь фуийция передачи равна Е-

= а„(1ш') +

OiiM + Oo, (4.13.6)

то для прототипа с однородным рассеянием {dk=d, ft= 1,2,3,п) та же функция при (i)=0 равна

(4.13.7)

Где функция £j/£2 соответствует определению, данному в § 2.10. Обычно d является очень малой величиной, так что можно ограничиться только двумя последними членами в выражении (4.13.7).-Тогда легко показать, что

(AZ.A) = 201g(C d+l) 8,686C d, дб, (4.13.8)

где (Д/.а)о -приращение затухания в децибелах а частотею = 0 для случая, когда dO, по сравнению с затуханием при d=0 (т. е. когда в схеме отсутствуют потери)). В выражении (4.13.8) имеем С„=а,/ао, где а, н Оо - коэффициенты полинома в ур-нии (4.13.6).

В случае использования прототипов нижних частот при расчете .полоснопропускающих фильтров (Д1.а)о будет приращением затухания в середине полосы пропускания соответствующего полоснопропускающего фильтра, обусловленным конечной величиной добротности .резонаторов. Для фильтров верхних частот, рассчитанных из прототипов нижних частот, {ALa)o связывается с затуханием при ш- -оо. Уравнение (4jl3.8) справедливо как для фильтровтпрототнпов (рассмотренных в § 4.05), характеристики которых при отсутствии потерь имеют точки, где / а=0, так и для согласующих цепей протогипов (рассмотренных в §§ 4.09-4.I0). которые даже прн отсутствии потерь не имеют нулевых значений La ни иа одной из частот.

В табл. 4.il3.1 приведены значения коэффициентов С„ для прототипов с максимально плоскими характеристиками затухания, имеющих затухание 3 дб на частоте со,-1, а на рнс. 4.13.2 их графики для фильтров с чебышевскимн -характеристиками и функции величины пульсаций в полосе пропускания. В этом случае граничная частота полосы пропускания ы\ также равна единице. Следует отметить, что при пульсациях выше 0,3 дб кривые имеют падающий характер при п-четном и возрастающий - при п-иечет-ном. Это объясняется тем, что на частоте ю'=0 чебы.шевскин фильтрарототип при четном п имеет максимум пульсации (вершину выпуклости) кривой затухания, а соответствующий фильтр с нечетным п - минимум пульсации (впадину). Очевидно, что

*) Например, чебышевсжий фильтр с пульсацией 0,5 дб и с п=4 и^меет затухание /.А=05 дб при ш'=0. Если ввести однородное рассеяние, то затухание на частоте о)=0 будет равно iA=0,5-f (A-aIo, дб.

ТАБЛИЦА 4.I3.I

КОЭФФИЦИЕНТЫ С„. ИСПОЛЬЗУЕМЫЕ В Ф-ЛЕ (4.i3.B) ДЛЯ ФИЛЬТРОВ с МАКСИМАЛЬНО ПЛОСКОЙ ХАРАКТЕРИСТИКОЙ ЗАТУХАНИЯ

эффект .рассеяния / наиболее резко .проявляется Б минимумах равнопульсирующей кривой sary.faraiH.

Боде [19] получил выражение для приращения затухания при однородном рассеянии в виде функции крутизны фазовой характеристики (для функции ослаблееия по напряжению) и коэффициента рассеяния d. Это выражение мелеет быть преаставлено в виде

;8,686d дб,

dti)

4> = arg~

(4.13.9)

(4.13.10)

й &La - приращеиие затухания на частоте ш', на которой (вычисляется крутизна фазовой .характеристичси rf(f/dtt>).

Таким образом, выражение Боде оказывается очень удобным, ее. нужно оценить влияние однородного рассеяния на iroeofi частоте. Боде в своей работе [19] отмечает, что для случаев, когда в схеме все ин-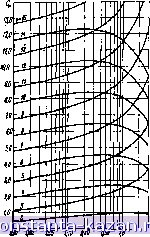

Рис 4.13.2. Зависимости значений коэффициента Сп для прототипов с чебышевской характеристикой от величины пульсаций в полосе пропускания.

Прн ы' =1

различном чнс.ч( элементов

реактивных

*) Из выражений (4.13.8) и (4.13.в) следует, что коэффициенты Сп в табл. 4.1Э.1 rf на рнс. 4.13.2 равны групповой задержке в секундах, когда частота ы' равна Нулю.

дуктивноси! Емеют одинаковую добротность Q=Qi, и все емкости - добротность Q=Qc, то хорошие результаты могут быть получены прн определении d .по формуле

d=2ii,l(QL+Qc). Кон [20] предложил другую формулу, которая удобна для оценки влияния потерь рассеяния в прототипах нижних частот при ()=0. Она может быть представлена в виде

{Мл )о = 4,343 V di£k. дб, (4.13.11)

где dft -определяются равенством (4.13.3), а значения элементов прототипа gk пронормированы таким образом, что go=l (как было сделано для всех прототипов, рассмотренных в дайной главе). Следует отметить, что эта формула справедлива и при иеодиород-ном рассеянии (когда коэффициенты рассеяния элементов различны).

Выражение (4.il3.11) было выведено в предпо.тожеини, что сопротивления нагрузки и источника равны 1 ом а что действие каждого элемента i?j или в схеме на рис. 4.13.1, на частоте т'=0 эквивалентно действию делителя напряжения нли тока соответственно образованного таким элементом и сопротивлением в 1 ом [20]. В связи с этим выражение (4.13.11) может привести к довольно значительной погрешности, если сопротивления нагрузки и источника не равны друг другу. Однако результаты будут вполне приемлемы, когда нагрузки равны нли, по крайней мере, отличаются незначительно').

ТАБЛИЦА 4.13.2

СРАВНЕНИЕ ВЕЛИЧИН (-- 1а. ВЫЧИСЛЕННЫХ ПО РЛЗЛИЧНЫ.Ч ФОРМУЛАМ ДЛЯ РЯ,ДА ЧЕБЫШЕВСКИХ ФИЛЬТРОВ С ОДНОРОДНЫЧ РАССЕЯНИЕМ

) Уравненне (4.13.М) может стать более точным для случая неравныч нагрузок, если его правую часть умножить на 4 o/? +,/<o-(- n+i), где /? и ?п-ы - ссгаротивления нагрузок. Это можно показать, применяя отличный от используемого здесь подход к вопросу (см. § 6.14).

В табл. 4.13.2 сравнивается точность выражений (4.13.8), (4 139) и (4.13.11) для различных чебышевских фильтров с однородным рассеянием. Случаи от 1 до З-го, которые относятся к Аильграм с числом реактивных элементов (1=4, соответствуют неравным нагрузкам, следовательно, ф-ла (4.13.11) имеет отиоси-гетьно низкую точность при высоком уровне пульсаций в полосе пропускания. Формула (4.13.8) не дает высокой точности при очень низких Q. Это связано с тем, что используются только два последние члена ур-ния (4.13.7). Точное зрначение (Д/.а)о было вычислено путем учета большого числа членов в указанном уравнении. Для вычисления по ур-нию (4.13.9) вначале из рис. 4.08.1 была определена крутизна фазовой характеристики. Следует отметить, что при этом получены весьма хорошие результаты. Включенный в табл. 4.13.2 пример с добротностью Q=10 представляет практический интерес, так как для полосовых фильтров с узкой относительной шириной полосы пропускания соответствующие им прототипы нижних частот будут иметь элементы с очень низкой добротностью [см. ур-ние (4.13.2)].

Приведенные выше рассуждения позволяют оценить влияние паразитных потерь рассеяния иа затухание в точке т'=0. Возникает важный вопрос о том, каково будет их влияние иа затухание во всей полосе пропускания? Выражение (4.13.9) позволяет получить иа него приближенный ответ. Из этого выражения следует, что д^-а из какой-либо частоте пропорционально крутизне фазовой характеристики (т. е. групповой задержке) иа той же частоте. Поэтому можио оценить ЛА-л во всей полосе пропускания, исследуя крутизну фазовой характеристики в данной полосе. Из графиков на рис. 4.08.1 видно, что обычно крутизна фазовой характеристики велика вблизи граничной частоты. Так, для уровня пульсаций 0,5, 0,01 дб и для случая максимально плоской характеристики крутизна вблизи этой частоты будет больше крутизны иа частоте с./ = 0 в 2,66, 1,73 и 1.40раз соответственно. Следовательно, д/.л вблизи граничной частоты будет больше, чем (Л/.а)о иа частоте и'=0 примерно во столько же раз. Эти результаты являются типичными, и в ряде практических случаев будут полезны при оценке ожидаемых результатов.

4.14. Приближенный расчет затухания прототипов в полосе аапирания

Кои [20] дал удобную формулу для вычисления затухания фильтров нижних частот в полосе запиранпя. Эта формула получена в предположении, что реактивные сопротивления последовательных индуктивностей значительно больше реактивных сопротивлений параллельных конденсаторов. При соблюдении указанного условия напряжение на каком-нибудь узле фильтра может быть определено с достаточной точностью по напряжению на пре-Дыдуи1е11 узле, если рассматривать элементы фильтра как эле-- 141 -

менты делителя напряжения [20]. Далее Кон упростил формулу, приняв, что ((oLftCft.,-1) r!m2Z.ftCft+,.

Формула Кона, представленная с помощью системы обозначении, принятой здесь для элементов фильтров-прототипов нижних частот, имеет следующий вид:

Ly, =201g[(m) (g-i2g3. f*-*-)

где go, g....., grt+i - значения элементов прототипа, показанные

на рис. 4.04.1а и б, а т'-частота в радианах, которая для получения высокой точности должна быть в несколько раз выше граничной частоты фильтра-прототипа.

В качестве примера рассмотрим чебышевский фильтр с числом реактивных элементов п=4 и .величиной пульсаций 0,2 дб. Из табл. 4.05.2 находим, что значения его элементов равны: go=l; g,= 1,3028; g2= 1,2844; §-3= 1,9761; g4=0,8468; 5= 1,5386 и граничная частота ш, = 1. Из выражения (4.14.1) с точностью логарифмической линейки получаем

La = 201g[(M) -4,29]-101g6,15. (4.14.2)

Расчет по ф-ле (4.14.2) для частоты т'=3 дает Z.a=43,1 дб. Из рис. 4.03.6 находим, что фактически затухание при этом равно 42 дб. Повторяя расчет для т'=2, получим /.л=28,8 дб, тогда как определение с помощью рис. 4.03.6 дает /.л=26,5 дб. Таким образом, оказывается, что даже для u7m,=2 ф-ла (4.14.1) дает достаточно хорошие результаты. Погрешность при ш'=2 равна -1-2,3 дб, а при ш'=3 - всего -t-1,1 дб

В выражении (4.14.1) пренебрегают влиянием рассеяния в цепи. Это справедливо только в предположении, что диссипативные элементы прототипа расположены, как на рис. 4,13.1. Такое расположение диссипативных элементов обычно свойственно прототипам для фильтров нижних частот, полоснопропускающих фильтров и фильтров верхних частот. В случае же прототипов для по-лоснозапирающих фильтров долж.но быть использовано другое расположение диссипативных элементов (см. § 4.15). При этом ур-ние (4.14.1) будет уже несправедливо в некоторой части полосы запирания.

4.15. Представление прототипов при учете потерь рассеяния в полоснозапирающих фильтрах

В случае полоснозапирающих фильтров паразитные потери в их элементах более резко в-таяют на .характеристику в полосе запирания, чем в полосе пропускания. В полосе запирания обычно существует одна илн несколько частот, на которых фильтр, не имеющий потерь, обладает бесконечным затуханием. Однако потери рассеяния в резонаторах приводят к уменьшению затухания. Прн этом возможно, что в некоторых случаях затухание в полосе - 142 -

-. Сьт;ГсГган1Гпр^?о:%Т^Гни';ГасГГ Тко*учес7ь влияниГко^ечн'ых добротностей резонаторов на максимальное затухание в полосе запирания.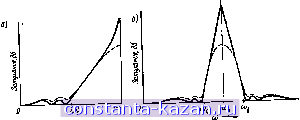

w - .

Рис. 4.16.1. Характеристика прототипа нижних частот (а) и соответствующая характеристика п&чоснозапнрающего .фильтра (б)

На рис. 4.15.1а сплошными л-нниями показана чебышевская характеристика прототипа нижних частот, а на рис. 4.15.16 - соответствующая характеристика полоснозапирающего фильтра для случая, когда .потери от-

сутствуют. Обычно резо-

наторы его настроены на центральную частоту полосы запирания (в отличие от настройки на центральную частоту полосы - -

пропускания в полосно- Рис. 4.152. Расположение диссппативных эле-пропускающем фильтре). Ф'шьтре^прототнпе нижинч частот.

у j. 4. и.рс, предназначенном для расчета затучания в по-

с7т0 приводит к тому, j,q(,g запирания соответствующего полосноза-что влияние потерь паи- пирающего фильтра

более сильно сказывается на центральной частоте полосы запирания. Пунктирная линия иа рис. .4.15.1-6 показывает, как за .счет потерь в резонаторах сглаживается характеристика затухания полоснозапирающего фильтра. Аналогичный эффект в прототипе нижних частот характеризует пунктирная линия на рис. 4.15.1 п.

Легко видеть, что при таком влиянии диссипативных элементов на затухание .фильтра-прототаша, которое иллюстрируют кривые иа обоих рисунках, онн должны быть введены в схему прототипа в соответствии с рис. 4.15.2. Отметим, что в этом случае п.ри а)- -оо peaKTjfBHHe элементы оказывают незначительное влия.ине и цепь работает точно так же, как лестничная цепь нз активных сопро-- 143 -