где rf -функция поперечных размеров шолосковой линяй. Если t/bxiO и ш/Ь^0,35, то величина id/b будет зависеть только от ij/Xc, Эта зависимость приведена в табл, 5.04.1.

5.05. Па1>аллельно связанные линии и решетки из линий между заземленными пластинами

Во многих полосковых устройствах используется связь между параллельными проводниками. Такими устройствами являются направленные ответвители, фильтры, симметрирующие трансзфор-маторы, линии задержки в виде структур на встречных стержнях и т. д. Несколько примеров параллельно связанных линий показано на рис. 5.05.1. Конфигурации о, б и в применяются главным

ю

1 и 1 и

Рис. S.05.1. Различные конфри-ура-ции связанных пачосковых линий

образом в устройствах со слабой связью между линиями, а конфигурации г, д, е, и ж - там, где требуется сильная связь.

Характеристики этич связанных линий могут быть выражены через Zfy, и Zoo - волновые сопротивления для четного и нечетного типов колебаний. Величина Zoe определяется как волновое сопротивление одной из половин связанной линии (одного из двух внутренних проводников линии относительно наружных заземленных пластин), когда токи в обоих внутренних проводниках равны и имеют одно направление. Величина Zoa является волновым сопротивлением одной из половин линии, когда токи во внутренних проводниках равны, ио протекают в противоположных направлениях. На рнс. 5.05.2 изображена конфигуращия электрического поля в поперечном сечении связанной линии, показанной на рис. 5.05.1а, при возбуждении в ней четного и нечетного типов колебаний. - 166 -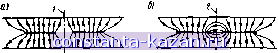

Рнс. 5.05.2. Распределение ишя для четного (а) и нечетного (б) типов колебанш в связанной полосковой линии. 1-ось четой симметрии; S-ось нечетной симметрии (потенциел земли)

Полосковые линии с Тонкими проводниками. Точное значение волнового сопротивления четного типа колебаний для полосковой конфигурации с бесконечно тонкими внутренними проводниками (рис. 5.05.1а) вычисляется по формуле [4]:

Ш К {К)

Z , = -

I Ег к (А.)

(5.05.1)

где

(5.05.3)

и вг - относительная диэлектрическая проницаемость среды. Точное значение волнового сопротивления нечетного типа колебаний для этого случая вычисляется по формуле [1]

ЗОд K(ko)

(5.05.4)

(5.05.5) (5.05.6)

а К - полный эллиптический интеграл первого рода.

Удобные таблицы значении K(k)IK(k) были составлены Обер-хеттингером и Магнусом [5]. На рис. 5.05.3 представлены номограммы для определения волновых сопротивлений четного и нечетного типов колебаний.

Полосковые линии с тонки.ии проводниками, связанные через щель. Величина Zoo для конфигурации в виде двух линий с тонкими полосковыми 1Проводиика.ми, разделенных тонкой стенкой (рис. 5.05.16), равна волновому сопротивлению Zq одиночной (несвязанной) линии (см. § 5.04). Волновое сопротивление четного типа колебаний Zoe Приблизительно подсчитывается по формуле

(5.05.7)

2 - -167 -

[mil I -

1 % S

где

/Гг К {к)

(5.05.8)

(5.05.9)

(5.05.10)

Полосковые- линии с круглыми внутреннилш проводниками. Волновые сопротивления четного и нечетного типов кооебаний для линий с круглыми внутреннитии проводниками, расположенными посередине между наружными пластинами (рис. 5.05.10), определяются нз приближенных выражений:

In Cth :

(5.05.11) (5.05.12)

Эти формулы должны давать хорошие результаты при d/b<0,55 и s/b>2d/b.

Полосковые линии с двумя тонки.ии внутренними проводника-.VU, перпендикулярными к наружным пластинам. Волновые сопротивления связанных линий с тонкими проводниками, показанных иа рис. 5.05.1г, приблизительно вычисляются по формулам [6]: 188,3 К {к)

Z =

296.1

Vir К Ik) 1

Ver - .(г cos * + In -

(5.0513) (5.05.14)

где k=\ 1-fc a К - полный эллиптический интеграл первого рода. Отношение ш/Ь равно

Arctg

--Arth

к s k b

к b

(5.05.15)

Обратные тригонометрические функции вычисляются в радианах в пределах от О до л/2. Чтобы определить размеры линий для заданных значений Zee и Zoo, вначале находится значение k из ф-лы (5.05.13) и таблиц K(k)IK(k) [5]. Затем по ф-ле (5.05.14) вычисляется значение b/s-и, наконеи, по ф-ле (5.06.15)-значение ilb. Значения w/b и s/b, вычисленные по этим формулам, будут - 159 -

достаточно точными прн условии, чго величина w/s больше едпницы.

Полосковые линии с овумя тонкими внутренними проводниками, параллельными наружным пластинам. Формулы волновых сопротивлений четного и нечетного типов колебаний для связанных линии, показанных на рис. 5.05.16, оказываются предельно простыми при условии (ш/Ь)/(1-s/b)>0,35 [6]:

168.3,<

Zoe = ---

ш1Ь

(5.05.16)

+

l-s/b 188,3/1

wlb l~s/b

(5.05.17)

+ - -

Величина CJ представляет собой емкость на единицу длины с каждого края каждого полоскового проводника (т. е. краевую емкость), которую нужно добавить к плоскопараллетьной емкости, чтобы получить точное, значение полной емиости полосок относительно заземленных пластин для четного типа колебаний.

Величина С^ является аналогичной емкостью для нечетного

Рис. 5.05.4. Краевые емкости четного и нечетного типов колебаний для бесконечно тонких полосок, параллстьных наружным проводникам линии

типа колебаний; е, -относительная диэлектрическая проницаемость. На рис. 5.05.4 построены графики для краевых емкостей четного и нечетного типов колебаний.

Если внутренние проводники связанных линий (рис. 5.05.1а. г, d)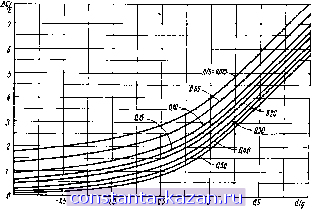

Рис. 5.05.Й. Емкость между полосковыми провод11Нка.М11 для конфигурации на (рис. S.OS.Ie.

Дли случая J/g>l емкость вычисляется из выражении

в е \die=\

имеют конечную толщину, то волновые сопротивления четного и нечетного типов колебаний несколько изменяются. Для учета конечной толщины мож1но пользоваться поправками Кона [7].

Полосковая конфигурация типа прокладка с тонкими проводниками. Эта конфигурация (рис. 5.05..1е), в которой две линии шириной с всегда на.ходятся под одинаковым потенциалом, особенно полеЭ1на при получении сильной связи с тонкими полосками. Полоски поддерживаются оаноролным диэлектриком с относительной диэлектрической проницаемостью ,ег, шолностью заполняющим область между наружными пластинами [32]. Размеры полосковых линий, со-

Рис. 5.05.6. Краевая емкость каждого из сдвоенных тонких полосковых проводников для конфигурации на рис. 5.05..1е (с нар|у1жной стороны)