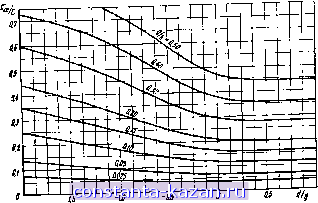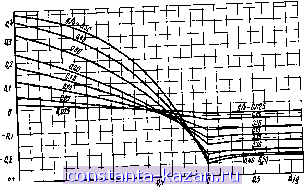ответствующие задан-ныы значениям Zoe Zqo мсймно найти с помощью графиков на рис 5.05.5-5.05.8. При этом необходимо использовать следующие ооотаошеяия:

376.6е

Co. 376,вв

(5.05.18) (5.05.19)

где Сое и Соо - полные емкости на единицу длины четного н яе-четвого типов колебаний либо для -полосок шириной е, либо для полоски шириной а. Абсолютная диэ.тектрическая проницаемость в равна 0,08855ег пф/см. Используя заданные значения Zoe и Zoo, вьшисляем величину ДС из следующего выражения:

ДС 188,3

poo Ql£

(5.05.20)

J

Выбираем значения 6 и g и нз рис. 5.05.5 находим d/g. Величины CJe и CJ,/e определяем из графиков на рис. 5.05.6 н 5.05.7; вместе с величиной Сое/е, вычисленной по ф-ле (5.05.18), подставляем их в ур-ние (5.05.21) и находим значение с/Ь:

(5.05.21)

Наконец, с помощью кривых на рис. 5.05.8 определяем значение Сае/в н затем, подставляя его в ур-нне (5.05.22), - значение а/Ь:

J-C jB~C-J.~OAi\

-(5.05.22а)

Таким образом, все физические размеры определены.

Формулы точны, если аЗ>й и сЗ>6, так как при этом не взаимодействуют краевые поля противоположных концов полосок. При а/Ь^0,Зб и [(с/6)/(1-g/6)]>0,35 точность приведенных формул составляет 1,24%. Если указанные условия ие выполняются, то можно ввести приблизительную поправку. Она основана на увеличении плоскопараллельиой емкости для того, чтобы компенсировать уменьшение краевой емкости из-за взаимодействия краевых полей. Если первоначальное значение щ/Ь оказалось меиыие 0,35, то можно использовать другое значение - аг/Ь, определяемое из ныражения

Да 0,07--gi№ , b ~ 1,20

причем должно выполняться условие 0,1<а2/6<0,-3б. Аналогичное выражение для коррекции первоначального значения С|/Ь имеет следующий 1вид:

с, l(i,m(l-gib)-cjb] b 1,20

6* 163 -

(5.05.226)

(5.05.22В)

Это выражение справедливо, когда д/Ь достаточно мало и O.KMby/O-g/b).

Если полосиа шир-иной а настолько глубоко введена между полосками шириной с, что rf/fi>I,0, то значения С^/е.и /е для четного типа колебаний остаются такими же, как и при d/b=l. Однако величина ДС/е изменяется. Ее можно вычислить, прибавляя величину 4(rf/g-1) к значению ДС/е при tl/g=lfl. Если .расстояние В/Ь между полосками шириной с больше, чем 0,6, или если ti/g<- 2,0, то более нод.ходящими, вероятно, будут конфигурации на рис. 5.05.In, б и в.

Полосковые линии с толстыми прямоугольными стержнями. Конфигурацию с толстыми прямоугольными стержнями (рис.

.4 Уг

Рис. 5-05.9. Нормириианиые краевая емкость четного тнпа колебаний С^е/е и емкость между свяэатпшми прямоугольными стержнями ЛС/е

5,05.Лж) можно также использовать для получения сильной связи между линиями [33]. Размеры проводников для заданных значений Zte и Zoo на.\одят нз графиков на pirc. 5.05.9, 5.05.IO и 5.05.11. Методика использования этих графиков следующая. Сначала из выражения (5.05.20) по известным значениям Zoe и Zqo определяем величину ДС/е. Затем выбираем значение t/b и по графикам рис. 5.05.9 на.ходим s/b. Размер w/b сатределяем нз уравнения - 104 -

I V П2 ез

US и 1.1 1.2 и 1.4 Vj

Рис. 5.05.10. Нормированная краевая емкость нечетного тнпа колебаний для прямоутольных стержней

1Л 1.0 D.S 0.1 04

Рис. 5.0Б.М. Нормированная краевая еиносгь для одиноч-кого прямоугольного стержня

2в

(5.05.23)

Емкость Со, вычисляем по ф-ле (5.05.18). Краевую емкость С, для четного типа колебаний можно найти из графика на рис - .!№ -

5.05.9, а емкость CJ - из графика на рис. 5.05.11. Кривые на рис. 5.05.10 позволяют непосредственно определить значение CJ.

На рис. 5.05.12 представлены различные краевые и плоскопараллельные емкости. Следует заметить, что краевые емкости нечетного типа колебаний CJ соответствуют краевым емкостям между внутренними краями стержней и металлической стенкой, помещенной посредине между стержнями. Из рисунка вядио, что полная емкость для нечетного типа колебаний равна

5l = 2

а для четного типа иолебаний

r£ -J---J--L

(5.05.24)

(5.0525

Нормированная плоскопараллельиая емкость иа единицу длины равна Cf/e=2w/ib~t), где е=0,08855Е,. пф/см.

Формулы н графики для краевых емкостей четного и нечетного типов колебаний CJ/e и CJ/e были получены с помощью метода конформных отображений. Они точны при [(w/b)/(l-t/b)]-oo. .Можно предположить, что прн [(w/b)/(l-t/b)]> >0,35 взаимодействие между краевыми поля.ми достаточно мало, так что значения Соо/е и Сое/е, полученные из выражений (5.05.24) и (5.05.25), больше истинных не более чем на 1,24%.

Бслн первоначальное значение w/b, вычисленное из ур-иия (5.05.23), окажется меньше, чем 0,35{1-{t/b)] (в этом случае краевые поля будут взаимодействовать), то следует использовать другое значение w/b, вычисляемое по формуле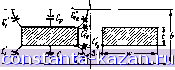

Рис. 6.05.12. Краевые и плоскопараллельные емкости связанной линии с пря1МОугольныгчи ироводниками

1,20

(5.05.26)

При этом должно выполняться условие

0,1<(ш7Ь)/[1-(*/6)1<0,35.

Несимметричные параллельно связанные линии. На рис. 5.05.13 изображена пара несимметричных параллельно связанных линий и показаны емкости их проводников. Величина Со представляет собой емкость на единипу длины между проводником а и землей, - 166 -

- -ос 1Г i

Ниш Ь

величина С^ъ - емкость на единицу длины между про-в иниками а и Ь, а Сб - д, .

>[,кость а единицу длины д,

между проводником b и ;ТЛ землей. Когда СпФСь, вол-

ОВЫе проводимости линий р 505,3 нес,.мметрич„а„ параллельно ак для четного, тагк и для связанная линия,

нечетного типов колебаний С^. Со,н С^, -емкости линии на единицу длины

ие .равны. Это отмечено в

выражениях (1) в табл. 5.05.1. Емкости четного и нечетного типов колебаний для ливии а можно представить следующи.м образом:

cs;,=c.-f2c, cg.=c..

(5.05.27)

ТАБЛИЦА 5.05.1

СООТНОШЕНИЯ МЕЖДУ ПРОВОДИМОСТЯМИ. СОПРОТИВЛЕНИЯМИ И ЕМКОСТЯМИ НА ЕДИНИЦУ ДЛИНЫ ДЛЯ НЕСИММЕТРИЧНЫХ ПАРАЛЛЕЛЬНО СВЯЗАННЫХ ЛИНИЙ

Сь+2СаЬ

С„Ч-2С^ vF

vF vF

e )e,V 2 )

с

= 3-10 *, 6r. см1сек - скорость света в среде распространения;

11с 376,7 OA - волновое сопротивление свободного пространства; е = 0,08855 Ег. -абсолкугная диэлектрическая проницаемость;

F = C Cb+CCa, + CbC,: - 167 -