 |
 |
 |
 |
|
Главная -> Согласующие цепи 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 [ 28 ] 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 а для линнн Ь: (5.05.28) Для симметрич'иых лараллельно связанных линий волновое сопротивление нечетного типа колебаний является обратной величиной волновой проводимости; аналогично и для четного типа колебаний. Однако из вы.ражеиий (2) в табл. 5.05.1 следует, что это несправедливо для несимметричных параллельно связанных ли-ний, сопротивления для которых не являются обратными величинами проводимостей. Дело в том, что определение проводимостей подразумевает возбуждение линий равными по величине напряжениями одного знака для четного типа колебаний и противоположных З'Наков для нечетного, а величины токов в двух линия.х могут быть не равны друг другу. При определении сопротивлений подразумевается возбуждение линий равными по величине токами одного знака для четного типа колебаний и противоположных знаков для нечетного, а величины напряжений в двух линиях могут быть не равны друг другу. Можно показать, что для несимметричных линий из-за этого различия граничных условий получаются неравные отношения напряжения к току. 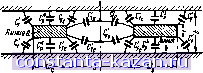 Рис. 6.05Л4. Поперечное сечение неС1шметричной параллельно связанной линии с -прямоугольньшн проводниками. Вертикальная штрнх-пунктирная линия показывает электрическую стенку для нечетного типа колебаинй или магнитную стенку для четного типа колебаний iHa рис. 5.05.,14 приведены легко рассчитываемые несимметричные параллельно связанные линии. Оба стержня имеют одинаковую толщину и предполагаются достаточно широкими, так что взаимодействие краевых (полей с правой и левой сторон каждого стержня пренебрежимо мало и.ти, по крайней мере, достаточно мало, чтобы его можно было учесть с помощью выражения (5.05.26). При этих условиях краевые поля обоих стержней будут одинаковыми, а неравенство емкостей С и Сь обусловливается целиком неравенством плоскопараллельных емкостей С° а CJ. Для структуры на рис. 5.05.14 имеем: c =2(C +c;-;c;j; C .= (C; -C;j; (5.05.29) c.=2(C*-fc;-fC;,). Расчет такой лиини по известным сопротивлениям или проводимостям четного н нечетного типов колебаний начинается с определения по выражениям (3) или (4) в 1а1бл. 5.05.1 емкостей Со/е, Саь/е и Сь/в. Задаваясь величиной t/b и зная, что =f. (5.05.30) с помощью графиков на рис. 5.05.9 определяем величины s/b и Cg/£ По графику на рис. 5.05.11 определяем величину С'/е, а затем вычисляем значения wjb н гюь/Ь по формулам: b 2 \ b I l~2 \ е ) б b 2 \ b jl 2 {f. j E E (5.05.31) (5.05.32) Так как расстояние между наружными пластинами b известно, легко найти ширину стержней и шь. Эту методику можно ис-(нользовать и при t/baiQ. Если Wa/b или Шь/Ь меньше, чем 0,35[1-(t/b)\ то для получения правильных размеров следует ввести коррекцию, используя выражение (5.05.26). Решетки из гшраллельно связанных линий. На рис. 5.05.15 изображена решетка из параллельно связанных линий, которая может j-f, ±,Ц Л.Сг -п /г т'г т= № Рис. 5.05.1S. Поперечное сечение решетки из лараллельно связанных линий быть использована в фильтрах на встречных стержнях (см. гл.10). В этой структуре асе стержни имеют одинаковое отиошеняе t/b, а остальные размеры стержней легко вычисляются, если обобщить методику расчета несимметричных параллельно связанных линий, показанных на рис. 5.05.14. Злектрические свойства структуры, изображенной нй рис. 5.05.45, могут быть охарактеризованы с помощью собственных емкостей на единицу длины каждого стержня относительно земли Ch и взаимных емкостей на единицу длины Ch,h+\ между соседними стержнями ft и k+\. Такое представление не всегда будет точным, ибо в некоторых случаях возможно сильное взаимодействие между полями элементов, не являющи-- 169 - ч мися соседними. Иначе говоря, краевая емкость между данным элементом (линией) и, напри.чер, элементом, находящимся за ближайшей соседней линией, будет значительной по величине. Однако опыт показал, что, по крайней мере, для геометрии структуры, приведенной на рисунке, это представление имеет удовлетворительную точность при проектировании таких устройств как фильтры на встречных стержнях. Для расчета рассматриваемых в книге структур в виде решеток из параллельно связанных линий будут получены уравнения для нормированных собственных и взаимных емкостей Cle и Ck,k+ile на единицу длины. Тогда поперечные размеры стержней и расстояния между ними определяются следующим образом. Сначала выбираем значения t к Ь. Затем, так как 4.t-bl то можно использовать график на рис. 5.05,9 для определения Sft, k+\lb. Таким способом находятся все расстояния ь, ii+i между стержнями. По графикам на том же рисунке определяются нормированные краевые емкости (Ср*,),+[/е, которые связаны с зазорами между стержнями Sk,k+i. Нормированная ширина А-го стержня равна afcJ /, J \ Г 1 /Ск\ (C ) .ki Ь 2\ Ь I \ 2\в I в в . (5.05.34) Для стержня на конце решетки (например, крайнего слева стержня на рис. 5.05.15) величину С^/е для наружного края сте.ржня следует заменить величиной С|/е, которая определяется из графика на рнс. 5.05.11. Таким образом, для стержня О (рис. 5.05.15) имеем Ь 2 V b / L 2 \ и I (5.05.35) Если ffiiu/b<0,35tl-((/Ь)] для какого-либо стержня, то ширина его корректируется согласно выраженню (5.05.26). 5.06. Основные свойства волноводов Широко используемым элементом фильтров свч является волновод, представляющий собой полый проводник, в котором может распространяться электромагнитная энергия на частотах, превышающих некоторую критическую частоту fc- В волноводе возможно распространение бесконечного числа волн типа ТЕ (поперечно-электрическне волны) или типа ТМ (поперечно-магнитные волны). Волны типа ТЕ имеют составляющую магнитного поля и не имеют составляющей электрического поля в направлении распространения. Волны типа ТМ имеют составляющую электрического поля - 170 - и не имеют составляющей магнитного поля в направлении распространения. Обычно волновод рассчитывают так, чтобы по нему распространялась энергия только одной волны; в этом случае его можно рассматривать как передающую линию с коэффициентом распространения VI и волновым сопротивлением Zq. Коэффициент распространения волновода определяется однозначно. Волновое сопротивление волновода можно рассматривать как волновое сопротивление по полю Z (т. е. отношение напряженности поперечного электрического поля к напряженности поперечного магнитного поля), умноженное на некоторую постоянную. Значение постоянной зависит от вида определения волнового сопротивления (т. е. могут использоваться либо напряжение и ток, либо напряжение н мощность, либо ток и мощность). Поэтому волновое сопротивление волновода не будет однозначной величиной, как для передающей линии с волной типа ТЕМ. Однако эта неоднозначность оказывается несущественной при расчете волноводных фильтров, так как можно всегда пронормировать все элементы эквивалентной схемы относительно волнового сопротивления волновода. В волноводе без потерь, заполненном диэлектриком с относительной диэлектрической проницаемостью Ег, длина волны в волноводе Xg, длина волны в свободном пространстве к, длина волны в диэлектрике Я н критическая длина волны } связаны соотношением я? ~ х= Ч (5.oai) Волновое сопротивление, которое для удобства мы будем считать равным волновому сопротивлению по полю, может быть выражено медующим образом: Щ=- для волн типа ТЕ, (5.06.2) Klg для волн типа ТМ. Коэффициент фазы волны, распространяющейся в волноводе, авен Р, = - , рад,ед.длиш. (5.06.3) Наиболее обычным типом волновода, используемым в фильтрах -вч, является прямоугольный волновод шириной а и высотой 6, работающий на волне ТЕю. В случае волиы типа ТЕ о критиче-\ая длина волны определяется из выражения т - 171 - Величина индекса m равняется числу полуволн электрического поля, укладыван>щихся по ширине волновода а. Критическая частота fc (в Ггц) связана с критической длиной волны Хс, измеряемой в сантиметрах, выражением (5.06.5) Основной волной для прямоугольного волновода, т. е. волной с наименьшей критической частотой, является волна ТЕщ. Основной волной для круглого волновода с диаметром D будет волна ТЕц, критическая длина волны которой равна 1,706D. Затухание, обусловленное потерями в медных проводниках, в случае волн типа ТЕ,, распространяющихся в прямоугольном волноводе, равно а для волны ТЕц в круглом волноводе: МТЕ„) = 3,80-10- , дб;ед.длины, (5.06.7) где частота / измеряется в гигагерцах. На рис. 5.06.1а показаны графики затухания для этих типов волн. Затухание, обусловленное потерями в диэлектрике, для любого волноводиого типа колебаний равно а^ 27.3tgfl дб1ед.длины. (5.06.8) где tg6 - тангенс угла потерь в диэлектрике. Ненагруженная добротность Q волновода,) равна где величина Qd зависит только от потерь в диэлектрике: Qd= tgft (5.06.9) (5.06.10) а величина Qc является функцией потерь в стенках BOflHOBOfla и отношения f/fc. Q.=. (5.06.11) ) Дополнительные сведения об использовании волноводов в качестве резонаторов приведены в § 5.08. 5<L
i.ii lip Й 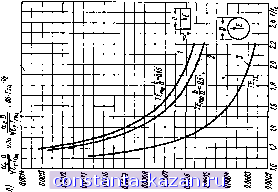 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© 2025 Constanta-Kazan.ru
Тел: 8(843)265-47-53, 8(843)265-47-52, Факс: 8(843)211-02-95 |