ности от генератора к rl равен

= Га=.

(1.04.4)

где Рт -максимальная мощность генератора (мощность отдаваемая в согласованную нагрузку);

Яг - мощность, отраженная от цепи фильтра.

Если сопротивление % слева на рис. 1.04.1а является положительным, то частотная характеристика коэффициента передачи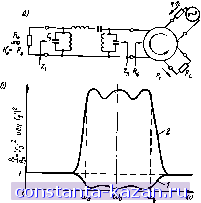

Рис. 1.04.1. Схема усилителя на отртшательном сс-протяаленнн с одиркуляторсм и согласующей цепью в виде полосового фильтра (а) и ее характеристики передачи (б)

мощности будет соответствовать кривой / на рис 1 04 16 При этом передача мощности ъ rl ъ .полосе .пропускания фильтра мала, так как Г1 = Гз тоже малы. Однако, если r заменить отрицательным сопротивлением Rl=~R, то коэффициент отражения слева будет равен

В результате получаем Гз

2i + j г,-д„

- 20 -

(1.04.5) (1.04.6).

При замене Rt, отрицательным сопротивлением -Rt, ц-иент отражен'ия Гз будет заменяться на ГП = 1/Гз .и фиииент передачи мощности будет соответствовать кривой 2 . рис. 1.04.16. ПрИ этих условиях мощность на выходе значительно превосходит максимальную мощность генератора на частотах в пределах полосы пронускання фильтра.

Таким образом, .используя выражения (1.04..1) и (1.04.6), легко рассчитать цепи связи для усилителей с отрицательным сопротивлением при помощи .методов расчета согласующих фильтров. Реальные приборы с отрицательным сопротивлением не являются Ч'исто активными сопротивлениями, эквивалентные схемы их содержат также и реактивные элементы. Например, для туннельных диодов основным реактивным элементом является относительно бо.1ьшая емкость, включенная пара.глелыно отрицательному сопротивлению. Удовлетворительная работа усилителя в диапазоне свч невозможна без специальной цепи связи, компенспрующеп влияние этой емкости. На рис.JJAAa R и С, могут рассматриваться как отр.ицательное сопротивление .и емкость ту-ннельного диода, а остальная часть полоснонропускающего фильтра - как широкополосная цепь связи.

Подобные пр.инц-пны также применяются при расчете широкополосных цепей связи для мазеров и параметрических усилителей. Однако в последнем случае расчет цепей связи несколько усложняется ввиду сравнительно сложных эффектов преобразования сонротивлепия элемента с изме,няющимися во времени параметрами [4, 7].

Цепь связи, показанная на рис. 1.04.1а, состоит из сосредоточенных элементов и поэтому не очень удобна для практической реа.тизащш в диапазоне свч. Методы, которые применяются для расчета практических структур свч фильтров такого назначения, рассматриваются в § 11.10 с ионольэова.нием результатов, полученных в §§ 11.08 и 11.09. Фильтры-Прототипы нижних частот для цепей связи в усилителях с отр.ц.цательным сопротивлением про-табулированы в § 4.11.

1.05. Цепи временной задержки и замедляющие структуры

Рассмотрим схему фильтра нижних частот, приведенную на рнс. 1.05.1а, для которого функция передачи напряжения равна EiJEe- Фазовая характеристика передаточной функции определяется как

Ф

- argрад.

Фазовая задержка фильтра на любой частоте равна

?р = - , сек,

ш

- 21 -

(1.05.1)

(1.05.2)

а групповая задержка

t. = . сек.

где ф - в рад; а ю -в рад/сек.

а) я. h

(1.05.3)

Рис. 1.05.1. Фнльтр нижних частот (а) и амплитудная и фазовая характеристики его шередаточ-ион фуниции (6)

iB различных задачах могут иметь значения оба вида задержки, однако именно групповая задержка определяет время, требуемое для прохождения сигнала через цепь [5, 6]).

Цепи нижних частот лестничной структуры, подобные схеме на рис. 1.05.1а, имеют нулевую фазу функции передачи при со=0; с увеличением ш фаза увеличивается. В пределе

(1.05.4)

где п - число реакшвных элементов в цепи. На рис. 1.05.16 показан возможный вид амплитудной характеристики передаточной функции ]Ео/Ее\ для рассматриваемого фильтра и приведена пр1иблизительио соответствующая ей фазовая характеристика. Заметим, что наибольший фазовый сдвиг имеет место в пределах полосы пропускания от ш=0 до (й=к>,. В этом случае групповое

) Если отсутствуют амплитудные искажения и dtp/dm яаляется постоянной велнчииой в пределах частотного спектра сигнала, то выходной сигнал будет точно соотаетстБОвать входному сигнал1у, но запаздывать во времени на ta сек.

время задержки в полосе пропускания таких фильтров может быть приблиэительно определено из формулы

1 = - .сек. (1.05.5)

2(1),

Конечно, в некоторых случаях величина id может заметно изменяться в пределах полосы пропускания, и выражение (1-05.5) оказывается весьма приближенным).

На рис. 1.05.2а показан пятирезонаторный полоснопропускаю-щий фильтр, соответствующий фильтру нижних частот иа рис. 1.05.1с, а на ряс. 1.05.26-его типичная фазовая характери-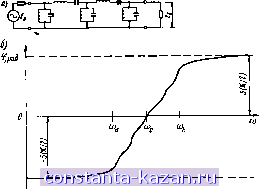

Рис. 1.06.2. Полоснопропуакающнй фильтр (а) и его фазовая характеристика (6)

стика. В этом случае полный фазовый сдвиг на частотах от (0=0 до ео=оо .равен пп, рад, где - число резонаторов; грубая оценка группового времени задержки в полосе пропускания дается формулой )

-сек. (1.05.6)

аъ - Ша

Здесь и еоь -граничные частоты полосы пропускания в рад.

) Так как в полосе пропусканнн фаза, как правило, не достигает своего макси\[ального зиачення, то время задержки по ф-ле (1.05.5) будет больше действительного (обьпио в два раза).

2) Так же, как и выражение (1.05.5), эта формула будет всегда давать завышенное значение времени задержки.

в следующих главах будет представлена более исчерпывающая информация о характеристиках временной задержки фильтров. Формулы (1.05.5) .и (1.05.6) приведены в этом параграфе просто для более полного изложения общих ее свойств. Предположим, что в некоторой системе желательно осуществить задержку импульсов в 10-саитиметровом диапазоне всти на 0,05 мксек и при этом полоса, необходимая для размещения спектра сигнала, при некотором изменении несущей частоты равна 50 Мгц. Если такую задержку осуществить с помощью воздушной коаксиальной лин'ни, то потребовалась бы лиирия длиной 15 м. Выражение (1.05.6) показывает, что эта задержка может быть получена с помощью пятирезонаторного фильтра, имеющего ширину полосы 50 Мгц. Спроектированный для этой цели полоснопропускающий фильтр 10-сантиметрового диапазона по длине будет меньше 30 см и может быть сделан весьма легким.

В замедляющих структурах представляют интерес: фазовая скорость

Ир = - (1.05.7)

илн групповая скорость

(1.05.8)

где - длина замедляющей структуры, г tp и id - величины, определяемые выражениями (1.05.2) и (1.05.3). Не все замедляющие структуры являются фильтрами, но большинство из них так кли иначе связаны с ними, например, волноводы с периодически раотоложенными емкостными или индуктивными диафрагмами, -линии со встречными стержнями и гребенчатые линии. Методы, -изложенные в этой книге, будут полезными для расчета таких замедляющих структур, которые в своей основе являются фильтрами. Применение фильтров в качестве цепей задержки рассматривается .в §§ 4.07, 4.08, 6.45, 7.09 и 11.11.

1.06. Применение теории фильтров для проектирования различных свч устройств

Из предыдущих параграфов следует, что наиболее общий подход, используемый при расчетах фильтров свч, применим также для оптимального проектирования самых разнообразных устройств диапазона свч. Вообще говоря, методы теории фильтров являются основными в тех случаях, когда необходимо обеспечить выделение, подавление и.ти разделение сигналов различных частот; когда ва-жно осуществить передачу с малым отражением энергии в пределах широкой полосы или .когда требуется обеспечить заданную величину времени задержки сигнала. Подобные задачи слишком многочисленны и разнообразны, что, разумеется, не позволяет - 24 -

рассмотреть здесь каждую из них в отдельности. Однако тель, ознакомившись с изложенными в книге общими метод расчета, вероятно не встретит затруднений при пользовании ими для решения целого ряда специальных задач.

Литература

1. в о d е Н. W. Network Analysis and Feedback .Implilier Design, p. p. 360-371 (D. Van Noslrand Co. New York, N. Y., 194S).

Боде Г. Теория цепей и проеитированне усилителей с обратной связью. Перевод с англ., под ред. А. А. Колосова н Л. .1. Мееровича. Издательство, иностранной литературы, М., 1948. .......

*2 FanoR М. Theoretical Liniitalions on the Broadband Matching of Arbitrary Impedance, Journal ol the Franklin Institute, Vol. 249, pp. 57-84 and 139-154 (January-February 1950).

Фано P. M. Теоретические ограничения полосы согласования произвольных нмпедансов. Перевод с англ. (н послесловие) Ю. Л. Хотуннева, под ред. Г. И. Слободенюка. М., Советское радио , 1965.

3 Valley G. Е. and W а П ш а п Н. Vacuum Tube Amplifiers, Chapter 2 and 4 (McGraw-Hill Book Co.. New York, N. Y., 1948).

4 Matthaei G. L. A Study of the Optimum Design of Wide-Band Parametric Amplifiers and Up-Converters, ШЕ Trans. PGMTT-9, pp. 23 -38 (January 1961).

5 G u i 11 e m i n E. A. Communication Networks. Vol. 2. pp. 99-106 and 490-98 (John Wiley and Sons, Inc, New York. N. Y., 1Ю5).

eiDi ToroMJ. Phase and Amplitude Distortion in Linear Networks. Proc. IRE, Vol. 36, pp. 24-36 (January) 1948.

7. Kun E. S. and Fukada M. Optimum Synthesis of Wide-Band Parametric Amplifiers and Converters, IRE Trans, РОСТ-8, pp. 410-415 (December 1961).

* Звездочками здесь и во всех главах, обозначена литература переведенная на русский язык.