Величина электрического дипольного момента р прямо пропорциональна произведению коэффициента электрической поляризуемости диафрагмы Р и напряжениости возбуждающего поля Еоп. В системе МКСА эта величина равна

р=ЕоР£о„и, (5.10.1)

где Ео = 8,855-10 ф1м, а п - единичный вектор, направленный от диафрагмы со стороны, противоположной возбуждающему полю.

Рис. 5.10.2. Магнитные дипо.тьные мшенты, индуцированные в диафрагме магнитным полем, парал.яе.ты1ььм плоскостн диафрагмы

Величина магнитного дипольного момента прямо пропорциональна произведению коэффициента магнитной поляривуемости диафрагмы М и напряженности тангенциального возбуждающего ма.гн тного поля Hoi- Для диафрагмы обычного типа, которая имеет оси симметрии, в системе МКСА эта величина равна

-m=MiHcJi+ МгНоЛ (5.10.2)

где и и V - единичные векторы, лежащие в плоскости диафрагмы вдоль осей симметрии; Ж, н - коэффициенты магнитной поляризуемости; Нои и Яо -напряженности возбуждающих магнитных полей

соответственно вдоль оси и и вдоль осн v.

Электрический дипольный момент р, индуцируемый в диафрагме возбуждающим электрическим полем, будет излучать мощность заданного типа колебаний во второй волновод, только если электрическое поле того типа колебаний, который должен быть возбужден, имеет составляющую, параллельную дипольному моменту р. Аналогично магнитный дипольный момент т, индуцируемый в диа|фрагме возбуждающим магнитным полем, будет излучать мощность заданного типа колебаний во второй волновод, только если магнитное поле того типа колебаний, который должен быть возбужден, имеет составляющую, параллельную магнитному дипольному моменту т.

Для того чтобы применить теорию Бета, необходимо знать коэффициент электрической поляризуемости Р и коэффициенты магнитной поляризуемости М, иMj диафрагмы. Теоретические зна-- 198 -

чеяия этих коэффициентов можно получить только для диафрагм простой формы. Например, для круглой диафрагмы диаметра d эти коэффициенты равны M,=M2=dPI6 и P=rf/12. Для длинной узкой диафрагмы длиной / и шириной w они равны PMi = (я/16)/ш2 при условии. Что составляющая возбуждающего магнитного поля параллельна узкому размеру (ширине) щели (что соответствует направлению v для этого случая), а составляющая возбуждающего электрического поля перпендикулярна к плоскости щели. Вычислены также и коэффициенты поляризуемости для эллиптических диафрагм. Кроме того, коэффициенты поляризуемости диафрагм других типов, которые слишком сложно вычислять, были измерены Коном [29, 30] в электролитической ванне.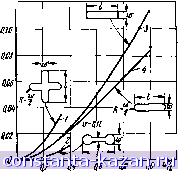

Рис. 5.10.3, Экспериментальные кривые для коэффициента элехтрнческоб поляризуемости.

/ - для крестообразной днвфрагаы; 2 -для гантельной диафрйгыы; я -дли прямоугольной днафрагаы; 4 -для прямоугольной диафрагмы с закругленными краями

На рис. 5.10.3 и 5.10.4 приведены графики измеренных значений коэффициентов поляризуемости для ряда диафрагм и теоретические кривые для эллиптических диафрагм. Легче всего выполняются круглые диафрагмы, но иногда нужны удлиненные, для того чтобы получить требуемую связь между прямоугольными волноводами.

Во многих случаях при рассмотрении линий передачи со связью через диафрагму более удобно оперировать эквивалентными схемами, а не нолями рассеяния. В табл. 5.10.1-5.10.2 приведены эквивалентные схемы некоторых четырехполюсиых и шести-- 199-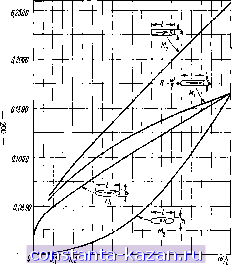

0.85

О Ш 0.2 В.З 0 5 US Ю 0.S 0,9

Рнс. 5.10.4. Козффициенты мапштной поляризувмости: о-для прямоугольной, эллиптической диафрагм и прямоугольной диафрагмы с закругленными краями; б-для Н-образной, гантельной и крестообразной диафрапм.

Кривые для эллиптичеекнл диафрагм - теоретические, асе остальные-экспериментальные. УакиЙ размер гантельной диафрагмы 0,1 /

ЭКВИВАЛЕНТНЫЕ СХЕМЫ И ОСНОВНЫЕ РАСЧЕТНЫЕ СООТНОШЕНИЯ ДЛЯ ДИАФРАГМ. СОЕДИНЯЮЩИХ ВОЛНОВОДЫ

Геометрия иеоднородиоетя

Поперечное сечение

Вид своку

ТАБЛИЦА 5.10.1

Эквиваяеитийя схема

Диафрагма, соединяющая прямоугольные волноводы одинакового поперечного сечения

В

-; M = M,cos 9 + M,sinqj;

г

-о

Пробо4женм табл. fiJO.J

ГСИМетр!.....ЕЮДИСфОДИОСТИ

JlojrepCHtiuL соч(.11ИО

Вид сбоку

Эквивалентная схема

Диафрагма, соединяющая прямоугольные волноводы разного поперечного сечения

ВрпнаП,д

Jiff

64л М=8№ - sin -

fl 1

fju bb X, >,g

==- ; /И = Ml cos Ф -(- Mj im ф; =

. 2

в

аЬ а..

4 я М sin -

I цеоднородностн

Поперечиое ceqeHue

Вид сйоку

Эквивалеетная схема

Диафрагаа, соединяющая круглые волноводы одинакового радиуса

Вина ТЕ,

-и

4 1 64лгм2