Пусть выражение (6.14.1) определяет амплитуду коэффициента отражения в (-ом резонаторе (секции), соответствующую ксв Si.-

(6.14.1)

Обозначим [12, 27] через Ui отношение потоков мощностей через поперечное сечение i-ro резонатора (секции):

[[Полный поток мощности 1 Ч- \Pi\

Полезный поют хющностн I - 1 Р( I

(6.14.2)

Рис. &I4.1. К опредсаднию ксв, наблюдаемыл изнутри отдельных сеиинй (резонаторов) трансформатора или фильтра.

Sy-ксв, который вндеи нэиутриг-го резонатора

Затухание линий передачи или диэлектрических сред обычно обозначается через а, но измеряется в различных единицах. Обозначим:

Old - затухание, измеренное в децибелах ка единицу длины;

о£ - затухание, измеренное в неперах j rfil4 3) на единицу длины; (b.H.d)

Оо -коэффициент поглощения

(используется в оптике [12])

Коэффициент поглощения Оо определяется как часть падающей мощности, поглощаемой на единице длины рассматриваемой системы. Таким образом, если / под - падающая мощность (или мощность излучения) в направлении z, то

(6.14.4)

Эти три коэффициента зат\хания ал, an и Оо связаны следующими соотношениями:

a = (101ge)a =4,343ao, дб a = (201ge)a = 8,686a , аб - 28 -

(6.14.5)

Обозначи.м длину I-ro резонатора и.ти секции через /(. Если каждое значение кратно четверти длины волиы при максимальном и минимально.\1 сопротивлениих на концах, как в случае синхронно настроенных на средней частоте ступенчатых фильтров и трансформаторов, то потерн рассеяния (если они достаточно .малые) определяются следующими выражениями [12]:

(1-роГ) а.Л'-/ S6

(Л/.л) -(1-р„р) V .t/., еп

(Ai.).-n-p.)Va.,W,( °)

(6,14.6)

где ро - амплитуда коэффициента отражения на входе-

Для того чтобы лО ф-лам (6.14.6) определить потери рассеяния, необходимо из ур-ния (6.14.2) найти для каждого резонатора (секции) отношение (у,- полного потока мощности к полезному Для полуволновых фильтров это особенно просто, так как

= hf- >. (6.14.7)

где Z; -сопротивление линии, образующей <-й резонатор, а n-fi -сопротивление на выходе полуволиового фильтра.

Сопротивления полуволнового фильтра Z; могут быть найдены таким же образом, как в пример / § 6.07 или как в примерах / и й 6.09, нли из рис. 6.03.1. Так как фильтр или трансформатор настроены синхронно, то справедливы следующие выражения-

5 = У„л.,

> 1

входной ксв 5 =-j* > 1

(6.14.8)

Ксв Si для любого из резонаторов синхронных фильтров можно записать также в иной форме:

S /JiLM,±s y, (6.14.9)

Наибольший индекс при V в этом уравнении равен п+1 (при любом 1) .

Узкополосные фильтры. Для фильтров с узкой полосой пропускания и большим значением R (фильтры с большим затуханием в полосе запирания) иэ выражений (6.09.2) в сочетании с ф-ламн (§ 4.03) для gi [7 следует, что величины Vt увеличиваются к середине фильтра (ср. табл. 6.10.1 или рис. 6.10.2). Поэтому в выражении (6.14.9) должен быть взят положительный показатель степени и, значит, этот же показатель будет во всех выражениях (6.14.8).

Тогда

V, = (1 = 1,2,. ., п+ 1). (6.14.10)

Так как фильтр согласован иа выходе (S +i=l), то из ур-ния (6.04.10) получаем максимально возможное значение ксв (в полосе запирания);

R = S (SA . .S f. (6.14.11)

Считая величину R постояниой (заданной), можно показать [12], что если произведения aj/j равны, го ур-иие (6.14.6) дает минимальные потери рассеяния при условии, что все S, также равны. Тогда все внутренние V,- (i=2, 3, п) будут одинаковыми и численно равны Квадрату li=V +i. У такого фильтра (называемого периодическим фильтром ) на средней частоте полосы пропускания будут Минимальные потери рассеяния для данного значения R (т. е. для данного максимального затухания в полосе запирания). Заметим, что в оптике такой фильтр дает максимальную коитрастиость . Общие формулы, справедливые также и для фильтров этого типа, получили Миленз [28 и Абелес [29].

Так как затухание Оп и ненагруженная добротность Qu связаны соотношением [30]

е„ is

то величина (&La)o может быть выражена через Q :

(A..)o=(.HP iv;5;-iW

(6.14.12)

(4..),= 27,28,l-p.P)jJi(f

- 290 -

Ui. дб

(6.14.13)

Чтобы связать этн уравнения с ур-нием (4.-13.11), необходимо предположить, что филыры имеют узкую полосу пропускания я большую величину R. Точно так же, как в гл. 4 и работе Кона [31], удобно пронормировать элементы фильтра-прототипа нижних частот, чтобы go=l. В ур-нии (4.13.2) и в указанной работе Кона W обозначает относительную ширину полосы пропускания по частотной шкале, которая связана с полосой Wq или wi, (см. §§ 6.02 я 6.03) волноводных фильтров с дисперсией следующим образом [32]:

<=i[jj или (6.14.14)

Можно показать, что в случае малых ш и больших R это приводит к следующ'Им выражениям:

(Д/,л)о = (1-р„Р)

(6.14.15)

(6.14.16)

(Л/.). = 4,343(1-1р.Р)-\], дб

(=1 /

Приведенные выражения отличаются от ур-ния (4.13,11) и уравнения в работе Кона [31] для фильтра нижних частот с сосредоточенными параметрами только дополнительным множителем следующего вида:

(l-PoP) = l/antilg[(Z.) /10I. Если добавить этот множитель в урниие (4.13.11) или .в ур-аие (1) у Кона (31], то они статут более точными. Так, например, умножая на него последний столбец в табл. 4.13.2, мож1н0 получить лучшее приближение к точным значешиям [в первом столбце для (/.а)о1 и умешьшить ошибку 1В каждом случае на порядок.

Формулы (6.14.6) являются самыми точными из имеющихся выраже.яий для потерь (рассеяния иа средней частоте полосы пропускания четвертьволнового ли полулволнового фильтра и могут быть применены иепосредственно к любому фильтру та/кого типа. Формулы (6.14..15) являются мамболее точными из имеющихся выражений для иотерь рассеяния полоснопропускающих фильтрах, полученных из фнльтров-Ш'рототипов нижних частот с .сосредоточенными параметрами (см. гл. 4). Формулы (6.14.6) и (6.14.15) 10 - 291 -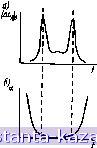

Рис. 6.М.2. Зависимссть потерь рассеяния (Д^х)о (а), суммы потерь рассеяния н потерь иа от-ражелие а (6) от чм-тоты

определяют потери рассеяния в середине полосы пропускания. Потери рассеяния обычно остаются довольно постоянными в боль-шеЛ части полосы пропускапня и имеют острые hhkii вблизи ее границ (см. рис. B.I4.2Q). Если полное затухание (потери иа отра-же 1пе плюс л терн .рассеяния) показать графически в функции частоты, то IB общем случае ха.рактернстика будет такой, как .на рис. 6..14.26; два вы€ту1па> тоявились благодаря двум пикам .потерь рассеяния .на рис. 6.14.2й.

Появление двух ликов потерь рассеяния вблизи границ полосы пропускания может быть связано с возрастанием внутренних полей и токов. Таким образом, следует ожидать, что прк измеиеннн частоты допустимая мощность фильтра будет изменяться приблизительно обратно пропорционально потерям рассеяния. Уве.тиче-ние запасенной энергии для согласованного фпльтра, в свою очс-ред, связано с уменьшением групповой скорости [32] или увеличением групповой задержки. Поэтом> следует ожидать, что групповая задержка фнльтра при изменении частоты будет изменяться приблизительно прямо пропорционально потерям рассеяния. Об этом уже упо.мнналось в § 4.13. Вопросы групповой задержки рассматриваются в § 6.15.

Пример 1. Заданы параметры полуволнового фильтра: Zj = l; Z;= 245,5; Z=0,002425; Zj =456,8; Z; =0,0045; Zj =1,106 (они соответствуют фильтру без потерь с no.iocoft пропускания шл = = 0.00185 и с величиной пульса1цин в ней 0,01 дб).

Вычислить потери рассеяния на средней частоте полосы пропускания, если фильтр выполнен на волноводе с затуханием 0,1329 дб1-ч. Длина волны ло=3,65 см; Ширина волновода а = =25.781 мм (см. также примеры / и 2§ 6.15).

Длина волны в волноводе равна

Jij = 5,166 см

Пз ур-ния (6.14.7) определяем значения ксв для каждого резонатора (секции):

Si-Z;/Z,- 222,0;

S, = Z-/Z = 455,8; S, Z-Z- = 412,5; S, -Z-.Z -245,5;

S5 -1,0 (no определению). Суммируя эти значения, получаем

0,- V5i= 667,9).

) Приближенное р.шеистоо следует из выражении (6.14.2) при S, l {прим. ред.).

Так как на средней частоте значение ксв на входе фильтра равняется Zj 1,106, то

р„ = 0.0025.

Следовательно,ИЗ первого ур-1ния (6.14.6) получаем (Л/,л) = 0,9975 2,583-667,9 = 2,29 вб.

6.15. Групповая задержка

Крутизна фазо-частотной характеристики согяасонаииого фильтра определяет его групповую задержку. Этот вопрос уже рассматривался в § 4.08, и полученные результаты для некоторых типичных фильтров-прототипов нижних частот с числом элементов п=5 приведены на рис. 4.08.1 и 4.08.2. В этом параграфе групповая задержка, потери рассеяния и допустимая мощность будут расматриваться для фильтров со ступенчатым изменением сопротивления таких, как, например, четвертьволновый трансформатор-прототип.

.Можно показать [33], что групповая задержка на средней частоте fo для однородного согласованного чегвертьволиового трансформатора определяется соотношением

(6.15.1)

где Id - крутизна фазовой характеристики которая может

рассматриваться как групповая задержка .в полосе пропускания (как Обычло, она будет именоваться групповой задержкой также и за пределами полосы пропускания, хотя ее физический смысл становится не соисем четким, если затухание резко изменяется от частоты).

Групповая задержка полуволнового фильтра ровно в два раза больше, чем у его четвертьволнового трансформатора-прототипа. В обшем случае групповая задержка льобого согласованного ступенчатого фильтра на средней частоте определяется выражением [33]

(6.15.2)

Из ур-ний (6.16.2) и (6.14.6) следует, что когда р„=0 (фильтп ZTaTn\Z в^Г™ коэффициёнты Ттуха'

Д/.и=аХ,(ХА,)7. (6.15.3)

- 293 -