б. Полюсы затухания могут лежать в лкЛой части р-плоскости.

Л Если £g -ЭДС генератора с нулевым внутренним сопротивлением, то нули функции Z,n на рис. 2.04.1 будут частотами собственных колеба-ний цепи и должны, следовательно, соответствовать нулям функции затухания Т(р)>).

8. Если генератор напряжения Eg е нулевым внутренним со-гаротивленмЕМ заменить генератором тока /g с бесконечно большим внутренним сопротивлением, то частоты собственных колебаний цепи будут соответствовать полюсам функции Zi . При замене Т(р) на t(p)=IglEi нули функции Т'(р) будут опять частотами собственных колебаний, но теперь они уже соответствуют полюсам функции 1ы.

Рассмотрим на конкретных примера.ч применение изложенных выше свойств электрических цепей. Предположим, что пря.чго-

к о

Всепвяасы

р

О

Рнс. 2.04.2. Функция передачи напряжения четыреянслЕОснинэ в виде отрезка лшппг без потерь, четвертьволнового па

частоте ыо: а - распределение полюсов и пулей функции в р-плоскостп (по осп абсцисс отложена величина о); б - амплитудная характеристика функции (по осн ординат отложена величина ы)

угольник на рис. 2.04.1 представляет собой линию передачи без

ч T- :rz - о. ПредполТГ,м'далее

1Г0 Kg~HLф/.g, где Zo-волновое сопротивле 1ие линии. При этих

условиях функция .передачи .напряжения Т(р) имеет распределение нулей и полюсов на р-плоскости, как показано на рис. 2.04.2Q. Так как линия передачи является цепью с распределенными параметрами, то существует бесконечное число частот собственных колебаний и, следовательно, бесконечный ряд нулей функции Т{р)-У всех входных и передаточных функций число полюсов и нулей должНо быть равным, если учитывается и точка р=оо, В рассмат-риваемо.ч случае отсутствуют полюсы затухания на конечной плоскости, все они группируются в бесконечности. Функция 7(1ю)

смещаются влево, а полюсы остаются фикоирОваиными на бесконечности. При этом величина осцилляции функций [(ift))! уменьшается. Когда окажется, что Rg=?i.=.Zo, то нули сместятся влево к минус бесконечности и функция передачи примет простой вид;

=Т(р,=

,яр;21й„

(2.04.2)

а ее модуль r.(ico) при всех значениях p = im будет равен двум.

Из приведенного примера видно, что траиоцендентная функция имеет бесконечное число полюсов и нулей, которые сгруппированы в бесконечности. Полюса группируются вбл.иэи оси р=-ю, так что при соответствующем приближении к бесконечности в этом направлении eJ стремится к бесконечности. Приближение к бесконечности со стороны отрицательных эначеинй р=-о приводит С к нулю. С другой стороны, если приближаться к бесконечности в направлении оси p=iw, то модуль е будет всегда равен единице, но фаза изменяется. Это посгоя.нство модуля объясняется равным влиянием вдоль оси 1и нулей слева и полюсов справа. Расположение бесконечного числа полюсов и нулей в бесконечности образует так называемую существенную особенность функции.

На рис. 2.04.3(2 показан полоснопропускающий фильтр, использующий три резонатора из отрезков линий передачи, которые имеют четвертьволновую длину на частоте юо, а' ша рис. 2.04.36 - типичная функция передачи для этого фильтра. Она яв'ляется периодической и имеет бесконечное число полюсов и нулей. Частоты собственных колебаний [т. е. нули функции Т(р)\ расположены вблизи оси id) около частот icoc, i3ci)c, 15шо и т. д., на которых отрезки линии равны нечегаому числу четвертей волны.

При р=0 я на частотах р=12юо, 14юо, Шюо и т. д., для которых длины отрезков линий равны четному числу четвертей волиы, цепь разомкнута в последовательной ветви и замкнута накоротко в обеих параллельных ветвях. В соответствии со свойством 3 (см. выше) это приводит к полюсам затухания третьего порядка, как отмечено на .р.ис. 2.04.36. На рис. 2.04.3в показан примерный график 7 (ico). При изменении величин нагрузочных сопротивлений 2-1 аз

Rg н Rl частоты собственных колебаний [нули Т(р)] сдвигаются н форма кривой Г(1ш) в полосах пропускания и вблизи их изменяется. Однако расположетие полюсов затухания остается при этом неизменным (см. свойство 2).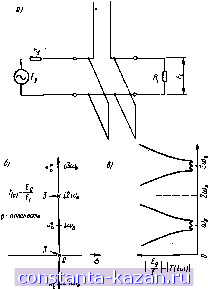

Рис, 2.04.3. Трехрезонаториый пс-лоснопропускающнй фильтр (а) и соответствующая ему функция передачи напряжения цепи: распределение полюсов и нулей (6}-, амплитудная характеристика (в)

Цепь, изображенную а рис. 2.(М.Зо, трудно реализовать практически с помощью экранированных линнй .передачи из-за последовательного разомкнутого шлейфа в середине цепи. Структура фильтра, показанная иа ряс. 2МЛ, более обычна и легко реализуется на практике. В ней используются коротко замкнутые, параллельно включенные шлейфы, соединевные отрезками линий пере-- 34 -

дачи, причем длина шлейфов и соединительных линий равняется четверти д.тины волны на частоте шо Эта цепь имеет такое же число собственных колебаний, как и цепь на рис. 2.04.3а, т может обеспечить аналогичную характеристику вблизи частот p=iwii,

Рис. 2.04.4. Полоснсшроиускающий фильтр с ко-роткозамкнутыми лараллельньши шлейфами, разделенными отрезками линий

i3coo и т. д. Однако иа частотах р=0, i2o)o, 14шо и т. д. цепь действует, подобно трем ороткозамкнутым цепям, включенным парал-тельно (что эквивалентно одной корогкозамкнутой параллельной ветви). В результате полюсы затухания на этих частотах являются полюсами только первого порядка. Таким Образом, можно заключить, что данный фильтр не будет иметь такой крутизны характеристики, как фильтр иа рис. 2.04.3а, полюсы которого иа оси ico являются полюсами третьего порядка. Соединительные линии также дают полюсы затухания, но как и в случае, раосмотрениом иа рис. 2.04.2, эти полюсы находятся в бесконечности. Они окя---очень малое влияние иа крутизну характериг- ответствует равное число нулей, кг- но ближе, и, следовате-

Приведениые пример ных колебаний и частот стики фильтра, содержа! ный анализ имеет зиачс!

2.05. Обобщенны!

В обозначениях рис. 2. четырехполюсника определ

или в матричной форме:

Л

* ё S i

° ё й s?**V(.

S Е g j$mmeBT распростра-

Яня на ед. ДЛИНЫ; а /олновое сопротивление t° лишш. ом

Рис, 2.05.1. Направления токов и на-йрякення нэ входе н выходе четырехполюсника

полюсников (рис. 2.05.2) матриц:

Эти лараметры являются особенно полезными, если необходимо-связать характеристики отдельных четы-рехполюсн-иков, включенных каскадно, с общей характеристикой каскадного соединения. Обобщенные параметры для двух каскадно включенных четырех-оп.ределяются путем умножения их

(CA+DA)(CA + OA).

(2.05.3)

Повторением этой операции могут быть вычислены обобщенные параметры для каскадного соединения любого числа четы-рех-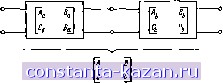

Рис. 2.05.2. Каскадное соединение двул четырелполюсннков

оолюсников. в табл. 2.05.1 приведены обобщенные параметры для ряда наиболее распространенных схем.

При определенных условиях обобщенные параметры удовлетворяют следующим соотношениям:

Если четырехполюсник взаимный, то

AD-BCl. (2.05.4)

Если четырехлолюсник симметричный, то

A = D. (2.05.5)

Если четырехполюсник ие обладает потерями (т. е. не содержит диссипативных элементов), то для частот p=ie> А т D будут чисто вещественными, а В и С - чисто мнимыми величинами.

Если у четырехполюсника на рис. 2.05.1 поменять местами вход и выход, то квадратная матрица в ур-нии (2.05.2) заменится на

(2.05.6)

таблица 2.05.1 ОВОЕЩЕННЫЕ параметры некоторых простых СХЕМ

Обобщенные параметры

A = i: B = Z;

С = 0; D=l

= 1; fi = 0,-

с = У: D = i

c = : = cbv,/.

где Y, = Ol -ф. i p, - коэффициент pacnponpa-нения на ед. длины; г„ - волновое сопротивление линии, ом

- ЗТ~