Rs и Rl частоты собственных колебаний [нули Т(р)\ сдвигаются и форма кривой 7 (1ю) в полосах пропускания и вблизи их изменяется Однако расположеиие полкхов затухания остается при этом неизменным (см. свойство 2).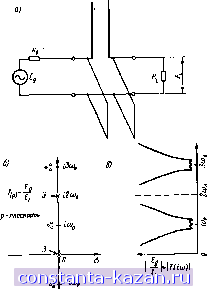

1200

Рис. 2.04.3. Трехрезоиаторнын ио-лоснопропускающий фильтр (а) н со-ответствуюшаи ему функция передачи напряжения цепи; распределение полюсов и нулей (6); амплитудная харахтеристика (в)

Цепь, изображе1нную на рис. 2.(М.За, трудно реализовать практически с помощью экранированных линий передачи из-за последовательного разомкнутого шлейфа в середине цели. Структура фильтра, показанная на рис. 2.04.4, более обычна и легко реализуется на практике. В ней используются короткозамкнутые, параллельно включенные шлейфы, соединенные отрезками .тиний иере-- 34 -

дачи, причем длина шлейфов .и соединительных линий равняется четверти длины волны иа частоте ио. Эта цепь имеет такое же число собственных колебаний, как и цепь иа рис. 2.04.3а ш может обеспечить аналогичную характеристику вблизи частот p=i(Oo,

Рис. 2.04.4. Полоснопропускающий фильтр с ко-роткозамкнутыми лараллельньши шлейфами, раз-дстенными отрезками -тнннй

i3(oo И т. Д. Однако на частотах р=0, i2mo, i4oo и т. д. цепь действует, подобно трем короткозамкнутым цепям, включенным параллельно (что эквивалентно одной короткозамкнутой параллельной ветви). В результате полюсы затухания яа этих частотах являются полюсами только первого порядка. Таким образом, можно заключить, что данный фильтр не будет иметь такой крутизны характеристики, как фильтр на ряс. 2.04.3с, полюсы которого на оси ieo являются полюсами третьего порядка. Соединительные линии также дают полюсы затухания, но как и в случае, рассмотренном на рис. 2.04.2, эти полюсы находятся в бесконечности. Они оказывают очень малое влинвие на крутизну характеристик, так как им соответствует равное число нулей, которые расположены значительно ближе, п, следовательно, сильнее влннют на характеристику.

Приведенные примеры иллюстрнруЕот алияиие частот собственных колебаний и частоты .бесконечного затухания на характеристики фильтра, содержащего отрезки передающих линий. Подобный анализ имеет эначекие при оценке той или иной структуры.

2.05. Обобщенные параметры четырехполюсника

В обоэначениях рис. 2.05.1 обобщенные (цепные) параметры четырехполюсника определяются уравнениями:

£, = Л£2-Ь В (-/,);

/i = C£j-bD;(-/,) (2.05.1)

или в матричной форме:

ТАБЛИЦА 2.06.1 ПАРАМЕТРЫ ХОЛОСТОГО ХОДА И КОРОТКОГО ЗАМЫКАНИЯ НЕКОТОРЫХ ПРОСТЫХ СХЕМ

Параметры хх и кз

Zb+Zc

- Ze g-f Zt

ii = Vi +3; й!>=-3; йI=-.,

У| + Уз

Z shY,r

Z shv,( cth Y,f Zo

где = 0( + P( ~ коэффициент распространения на ед. ДЛИНЫ;

Zp - вочновое сопротивление, ом

где параметры с индексом t относятся к полученному после такого преобразования четырехполюснику, а параметры без индексов - к исходному. В обоих случаях £i и /i соответствуют зажимам слева, а £2 и /2 - зажимам справа.

Для взаимного симметричного четырехполюсника можно, используя ур-ния (2.05.6), (2.05.3) и (2.05.4) и параметры А'.В'. С. D, относящиеся к его левой половине, получить матрицу его обобщенных параметров ъ виде

(\+2В'С') {2А'В') \2CD) (1-f 2В'С')

(2.05.7)

2.06. Параметры холостого хода и короткого замыкания четырехполюсника

В обозначениях рис. 2.05jl сопротивления холостого хода четырехполюсника могуг быть определены с помощью уравнений:

zi,/,-fZss/j = £2. (2.06.1)

Физически Z]i является входным сопротивлением со стороны зажимов 1-1, когда зажимы 2-2 разомкнуты. Параметр ziz может быть измерен как отношение £[ 2 три разомкнутых зажимах /-Смысл параметров г и пояшяется аналогичным образом.

Точно также, используя опять те же обозначения, можно определить проводимости короткого замыкания на основе уравнений:

yuEi+ytiEiI.

(2.06.2)

В этом случае i/n-проводимость со стороны зажимов I-i, когда зажимы 2-2 закорочены. Параметр У12 может быть вычислен как отношение Ii/E когда зажимы. /-/ закорочены н к зажимам 2-2 приложено напряжение £2.

В табл. 2.06.1 приведены параметры холостого хода н короткого замыкания для некоторых распространенных схем. Для взаимных четырехгаолюсников 2,2=25, и !/i2=S2i- Для четырехполюсников без потерь (г. е. состоящих только из реактивных элементов) параметры холостого хода и короткого замыкания являются чисто мнимыми величинами на всех частотах р=ш.

2.07. Соегеи

ння между обоби

ыии параметрами и параметраин холостоеЪ хода н короткого замыкания

Соотношения между обобщенными параметрами и параметрами холостого хода н короткого замыкания имеют следующий вид:

11 -яв so С = --=-=

гз, й1 тм zj, j/j, m,j

я toi газ, г„ j/

= = ={ га = = - = -

(2.07.1)

- Ун Л 1з =*Ц, = £. = ili.

л=ло-вс=

Л112

, (2.07.3)

взаимной цепи): (2.07.4) (2.07.5) (2.07.6)

( оо) no

Если любые 3 эгих параметров цепи выразить в функции коми-тексной частоты р, то они будут равны огношемню двух полиномов, каждый нз которых может быть записан в виде

полином = с (p-pi) (р-Рг) (р-Ра)

(2.07.7)

где с - вещественная постоянная, а р* - корни полинома.

Как можно ожидать из рассуждений, ириведеных в §§ 2.02- 2.04, расположеиие корней обоих полиномов в р-плоскости имеет определенное физическое значение. Величины, стоящие в правых частях ур-ний (2.07.1)-(2.07.6), введены с целью пояснеиия зтого значения.

Симнолами riis, п„ , п„, и п,о обозначены полиномы вида (2.07.7), корни которых являются частотами собственных колебаний цепи при условиях, указанных индексами s и о. Индексы означают; S - короткое замыкание, о - размыкание. TaiKHM образом, корни полинома riss являются частотами собственных колебаний цепи а рис. 2.05.1, когда вход и выход замкнуты накоротко, а корни полинома Лоо соответствуют собственным частотам при разомкнутых в.ходе и выходе. Корни полинома являются частотами собственных колебаний, когда левые зажимы разомкнуты, а правые- коротко замкнуты, а для. Пдо - наоборот. Символы ш12 и /Иат обозначают полиномы, корни которых являются полюсами затухания цепи (см. § 2.04), исключая полюсы зату.хания на частоте р = оо. .Полкном /П|2 имеет корни, соответствующие полюсам затухания при передаче от зажимов 2-2 к зажимам /-/ на рис. 2.05/1, а полином mji-корни, которые являются полюсами затухания при передаче от зажимов 1-1 к зажимам 2-2. Если четырехполюсник взаим1ный, то mi2=/n2i.

Рассмотренные полиномы для данной цепи связаны соотноше-

(2.07.8)

и дают определенные преимущества, когда используются в качестве основных параметров цени при описании ее характеристик[8]. - 40 -

Как видно из ф-л (2.07.4)-(2.07.6), определители Д, Д, и &у представляют собой рациональные функции от р, которые обязательно содержат сокращающиеся полиномы. Это может быть подтверждено использованием урний (2.07Л) -(2.07.3) совместно с соотношением (2.07.8). Сокращение общих множителей обычно уменьшает степень полиномов в указанных функциях примерно в два раза. АналогичЯые свойства будут справедливы и для цепи, содержащей элементы с распределенными параметрами, хотя при этом полиномы имеют бесконечную степень (см. § 2.02) и могут быть представлены трансцендентными функциями, такими, как shp и chp. Например, для л.иннн передачи без потерь:

/i, =n = Z ch = Z.fI

(2А-1К.

{[р -f- i(2ft-l)(0 l[p-i(2A-l)(i) ]};

2ТГП {--j l(P + i 2*. ) (p-i 2ftс.)]:

n =ZJsh; m = mi=Zo, (2.07.9)

где - волновое сопротивление линии, а шо - частота в радна-иах, для которой линия представляет собой четвертьволновый отрезок. В этом случае полиномы mi2=m2i не зависят от частоты, так как все полюсы затухания находятся в бесконечности (см. §2.04 и работу [8]). Выбор постоянных множителей для таких полиномов является в известной мере произвольным, в том смысле, что любому из них может быть приписано произвольное значение, тогда остальные постоянные множители определяются однозначно.

2.08. Падающая и отраженная волны, коэффициенты отражения и один вид коэффициента передачи

Предположим, что требуется рассмотреть передачу к зажимам 2-2 (рис. 2.08.1) с волновой точки зрения. По определению

где £,- -амплитуда падающей волны напряжения; £г -амплитуда отраженной волны напряження;

(2.08.1)

Рис. 2.06.1. Цепь (а) и ее замещение (6) с помощью теоремы об эквивалентном генераторе - 41 -