Пр)дояжвше табл. 8.01.t

ТипнчныЧ реэоиятор или секция фильтра

Иагрушюише

тгттттттттт Попоснобав лишв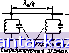

Основные свойства

Гребенчатый фильтр. Длина резонаторов / за. висит от величин нагружающих емкостей

так что фильтр может быть рас-

считан с очень широкой верхней полосой запи рання. Полюсы затухании расположены па ча

стогах и=0 и [0= - °- Предельно компактная

структура, которая может быть изготовлена без диэлектрических опор. Ненагруженная добротность резонаторов немного меньше, чем добротность резонаторов в фильтре 9 с теми же раэме-рамп сечения полосковых линий.

Расчетные данные для значений ш до 0,15 приводятся в § В.13

ф]пьтр с четвертьволиовычи связями между с^зонагорэчи. В чачег^с no.Vc.iiinx могут ис-..элыовагься объемные резоипторы, резонансные диафрагмы или резонансные контуры с сосредо-гочен11ь..1и элементами.

Расч гн1е цанные для значений w лорвдка 0,05 in;i меньше приводятся в § В-08

Цепь с сосредоточенными параметрами, которая и.101ьэуется при расчете фильтров свч с полу-сос,)едоточснными элементами.

Расчетные данные для значении w0,20 приводятся в § 8.11

Цепь с сосредоточенными параметрами, которая используегся при расчете фильтров свч с полусосредоточенными элементами.

Расчетные данные дчя значений ic<0.20 приводятся в § 8.11

Волноводные фильтры и фильтры из объемных резонаторов

Частота ospb будет прн Х^ Х^о/2. Однако если могут распространяться колебания высших типов, то характеристика в области верхней полосы запирания и второй полосы пропускания может быть искажена. Величина (La)ubb уменьшается С увеличением li: . Врлповодные резона-

Продолженав табл. S.OI.I

jfy Типичный реэокштчзр или секция фильтра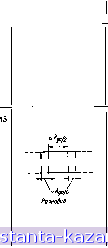

Основные свойства

торы дают относительно низкие потери рассея-ин для данной полосы w > .

В §§ В.06 и В.07 рассматривается расчет такн.\ фильтров для w 0,20. Вопросы, связанные с их расчетом при больших значениях Шх или при очень малых значениях Lr (например, 0,01 дб), а также с применением в иачестве фильтров верхни.х частот, излагаются в гл. 9

Использование четвертьволновых связей приводит к тому, что все диафрагмы почти одинаковы. Если сочленения выполнить в середине каждого четвертьволнового отрезка связи, то резонаторы фильтра можно легко испытывать отдельно. Частота ыврв будет при KgKgo/2. Однако в случае распространения колебаний высшп\ типов характернстшса в области верхней полосы запирания и второй полосы пропускания мо ет быть искажена. Вечичина (La)ubb уменьшается с увеличением полосы . Волноводные резонаторы дают для данной относительно низкие потери рассеяния. Удовлетворительная точность расчета будет при о\ порядка 0.05 нли меньше

Фильтр данного типа рассматриваетоя в §8.08

ДНЯ применения в качестве фильтров верхних частот свч диапазона. Хотя большинство фильтров табл. 8.01.1 выполнено из отрезков полосковых линий, многие из них легко изготовить в коаксиальном варианте (в обычной форме) нли в виде разъемной коаксиальной конструкции (см. гл. 10, рис. 10.05.3).

Одной из характеристик фильтра, представляющей интерес прн выборе структуры ПИФ, является средияя частота второй полосы пропускания, обозначенная в табл. 8.01.1 через iospb. Обычно она в два или три раза выше средней частоты шо .первой полосы fnpo-йускання. Однако для фильтра 8 частота iospb может быть боль-4ie Шо в пять или даже большее число раз. Фильтр 10 та1кже может иметь очень широкие (полосы затирания.

Все фильтры в табл. 8.01.1 имеют, по крайней мере, одну частоту (о, на которой затухание будет бесконечным (или точ'нее, оио было бы бесконечным, если бы не влияние потерь рассеяния). Этя точки бес-конечного затухания называют полюсами затухания (см. § 2.04), и оии могут быть лолюсамй первого или высш-его порядка. Чем выше порядок полюса, тем быстрее увеличивается затухание ло мере того, как частота пр№бл1ижается к частоте полюса.

Таким образом, по данны'м табл. 8.01.1, -в которой для каждого - 361 -

типа фильтра указаны порядок полюсов затухания и зиачания их частот, мож'но судить о величине затухания на различных участках полоссы запирания. У четырех фильтров {I, 2, 14 и 15) отсутствуют полюсы затухания на частотах выше средней частоты шер-вой полосы пропускан'ия шо и наибольшее затухание в полосе запирания между пертой и второй полосами пропускания ограии-чеио 31начениеМ {La)lsb, дб. Ка отмечеио в рассматриваемой таблице, макс,ималь ое затухатше {La)vsb в этих случаях -гъъжкт от ширины полосы пропускания w фильтра. Следует также отметить, что фильтры, у которых ,в полосе запирания, расположсииой выше (1)0, существует полюс затухания (первого порядка, могут иметь при какой-либо расстройке паразитные полосы лро'пуока-ния вблизи этого -полюса.

Другим критерием при выборе типа фильтра для конкретной задачи является величина иеиагруЖенной добротности Q резана-торов рассматриваемой структуры. ВоЛноводные или объемные резонаторы будут иметь более высокие ненагруже ые добротности и, следовательно, приведут к фильтрам с мниималь-ными вносимыми .потерями при дайной ширине полосы пропускания. Однако волноводные рез01наторы имеют существеины.й итЕцсстаток: они относительно громоздки и, кроме того, могут быть использованы только в отраБиченном частотном диапазоне изнза возмож-нооти вознИ1Ктовения колебаний высших типов волн. Поэтому там, где требуется широкая полоса протуокаиня или запирания, обычно предтючтитель'нее фильтры, выполненные либо из отрезков полосковый или коаксиальных линий, либо на полусосредоточениых элементах. Если используются конструкции из полосковых или коаксиальных линий, то наличие диэлектрика, оторый мож т быть необходим для мехаиического крепления, приведет к допол-.нительноиу уменьшению добротности резонаторов. В табл. 8.01..I отмечено, может ли быть вь полнена данная конструкция без ди-эле1Ктр.нче1ских опор или нет.

Фильтры, приведенные в таблице под номерами 1, 3, 9, 10 и 14, обладают характеристикалш, позволяющими удовлетворить самым различным требованиям многих задач'), а именно;

Фильтр 1 в коаксиальной форме обеопечивает очень простой 1И удобный путь реализации фипьтра пгевдоверхних частот. Промышленные образцы коаксиальных фильтров Бер.х!них частот в основном имеют именно такую форму.

Фильтр 3 наиболее ле-гао рассчаиывается н изготовляется в печатном виде, когда относительная ширина шолосы пропускания равна 0,15 или еще меньше. Однако его xapaKrepiHCTHKa в полосе запираиия и добротности резонаторов хуже, чем у екоторых дру-гих типов фильтров, приведенных в таблице, и выполненных в полосковой или коаксиальной форме.

*) Однако это не озна-iaeT, что именно данные пшы фильтров являются наилучшими во всеч случаям. Иногда какие-то требования рассматриваемой злдачн .могут быть .1учше удовлетворены другими структурами

Фяльтр 9 легко рассчитывается для любой ширины полосы лропуокания, очень комшактен и имеет высокое затухание в полосах затирания по обе стороны первой полосы пропускания.

Фильтр 10 компактен, расчет его прост, а кроме того, он может обекгпечить j)4eHb широкую верхнюю толосу запирания.

Фильтр /4 -ианболее простой .и распространенный т1Ш волноводного фильтра. При работе с одн.им (единСтвенным) типом колебаний такие фильтры обычно обеспечивают отличную характеристику.

8.02. Фильтры на связанных резонаторах')

В этом параграфе дается качественная оценка работы фильтров на связанных резо1Наторах. Для тех ч!итателей, которым в первую очередь приходится иметь дело только с практическим расчетом, а не с теорией, излагаемый матернал сопровождается примерами расчета конкретных типов фильтров. Подробный -выгод расчетных соотношеянй изложен далее в § 8.14.

В иастоящей главе ирн расчете будут использоваться прототипы фильтров с сосре1доточенными параметрами, рассмотренные н протабулнрованные в гл. 4. При этом можно обеспечить получение ППФ, и.меющнх приблизительно те же самые характеристики- чебы.шевоиу.ю'ИЛИ максимально плоскую.

Таким образом, .прототипу с оосредоточенными параметрами с чебышевской характеристикой (рнс. 8.02.1а) будет соответствовать ППФ также с чебышевской характеристикой (рис. 8.02.16).

Рис. 8.02.1. Характеристика прототипа ФНЧ (а) и соответствующая характеристика ППФ (б)

Многорезоиансность, присущая передающим линиям или объем-нити резонаторам, обычно приводит у яолосиопропускающих фильтров свч к поя1вленню дополнительных полос пропускания иа высших частотах, как это показано иа рис. 8.02.16.

) Рассмотрение фильтров на связанных резонаторах проводится здесь на основе под-чода. предложенного Коном [1]. Однако здесь этот подход излагается в более общем виде и применяется также к дополнительиьш типам фильтровых структур, ие рассмотренным Коном. По данному вопросу см. также работы к-в].

На рж. 8.02.2 приведена обычная схема протогмпа ФНЧ, а на рис. 8.02.3 - соогветствующая схема ППФ, которая может быть получена из прототипа частотным преобразованием, рассмотренным ниже в § 8.04.

Jir%

Рис. B.OlJ.a. Фильтр-лрототип нижних частот

п-нпепт п-чтн Рис. 8.02.3. Схема полосиопропускающего фильтра

Для параллельных резонаторов параметр ирутшзиы реактивной проводимости определяется из выражеви

6j=<o Ci = =*?Li/. (8.02.1)

Для последовательных резонаторов параметр крутизны реактивного сопротивления определяется из выражеш-ия

x =,coL,= - = -!- . (8.02.2)

Полоса пропускания и ее средняя частота определяются из выражений

(8.02.3) (8.02.4)

В этих -Еыражен'иях gj являются значениями элемеиточв лрото-ти-па; ш' и ы[ соогветсгвуют чейьршевской характеристике прототипа, как показано на рис. 8.02.1а, а частоты ш, шо, coi и ыг показаны на .чарактеристпке ППФ, гтриведенной ла рис, 8.02.16.

Ф-ильтр на рис. 8.02.3, разумеется, -не будет иметь дополнительных полос пропускания иа более высоких частотах (как на рис. 8.02.16), так как он состоит из элементов с сосредоточеиными параметрами - последовательных и параллельных резонансных контуров.

Стру-ктура, показанная на рмс. 8.02.3, практически очень трудно реализуется в диапазоне свч. Поэтому в свч фильтре более целесообразно использовать структуру, которая соответствует схеме, - 364 -

010= IcOiCOa.

приведенной на рис. 8.02.4, или ей дуальной. Здесь все резонансные контуры одного и того же типа, а эффект, связанный с чередованием последовательных и параллельных контуров, достигается с помощью инверторов сопротивлений , которые определены в § 4.12 и ойоз1начены ра рассматриваемой схеме в виде прямоугольников.

I-. Сг,

Рис. В.02.4. Схема полосиопропускающего фильтра, содержащего резонаторы. последовательного типа и инверторы сопротивлений

Такой полос'нопрапускающий фильтр может быть рассчитан из прототипа ФНЧ, приведенного на рис. 8.02.2. Вначале указанный прототип преобразуется в эквивалентный прототип ФНЧ, показанный на рис. 4.12.2а, который содержит только последовательные индуктивности и инверторы сопротивлений. Затем, применяя к этому эквиваленттому прототипу соответствующее частотное преобразование, уже определяют элементы рассчитываемого ППФ.

Практические способы приближенной реализации инвергорой сопротивлений будут рассмотрены в следующем параграфе.

Поскольку в диапазоне свч конструктивно трудно осуществить элементы с сооредоточенным'И параметрам:!- то обычно желательно реализовывать резонаторы на элемемгах с распределенными параметрами, а*не сосредоточенными, ьй\ это показано на рис. 8.02.3 и 8.02.4.

В качестве основных пара-метров, определяющ-их резонансные свойства резонаторов независимо пг их айда, удобно использовать и.х резонансную чацтоту шо и пара.четр крутизны.

Для любого резонатора в режиме последовательного резонанса (случай, когда на частоте то реактивное сопротивление равно нулю), используется параметр крутизны реактивного сопротивления, который определяется ьыражением

W, (8.02.5)

где X-реактивное сопротивление резонатора. Для обычшого последовательного LC-KOHTypa выражение (8.02.5) сводится к виду: x=(i)QL= 1/шоС.

Для любого резонатора в режиме параллельного резонанса (случай, когда на частоте шо реактивная проводимость равна нулю) используется параметр крутизны реактивной проводимости, который определяется выраженнем

b = о, (8.02.6)

2 dm щ

x=€i. 2 dm