метр 1И1Нвертора соггротнвлетия К здесь равен характеристическому сопротивлению (см. § 3.02) инвертирующей цепи и аналогичен в этом смысле волновому сопротивлению отрезка передающей линии. Все четыре схемы сох1раияют свойства инверторов в более широком астотном диапазоне, чем четвертьволновая линия).

На рнс. 8.03.2 токазаны четыре схемы с инвертирующими свойствами, которые представляют интерес при иопользовании их в качестве /-инверторов (t. е. инверторов, применяемых с резонаторами параллельного типа). Эти цепи дуальны цепям, приведенным на рис. 8.03.1, и параметры /инверторов являются характеристическими проводимостями инвертирующих цепей.

ТАБЛИЦА 8.03.1 ИНВЕРТИРУЮЩИЕ СВОЙСТВА НЕОДНОРОДНОСТЕЙ В ПЕРЕДАЮЩИХ ЛИНИЯХ

Схемы, предсталляющие неодиородиость

Ус ИМ

Основные СООТНОШЕНИЯ

- arctg--, рад

1 = У,

- arctg-, род о

, J o;

В табл. 8.03.1 показаны две схемы, также обладающие свойствами инверторов и полезные при определении инвертирующих свойств некоторых типов неоднородностей в передающих линиях. Примеры такого рода будут рассмотрены в §§ 8.05 и 8.06.

На рис. 8.03.3 показаш еще одни тип инвертора, содержащий отрезки передающей Л1инии с положительной и отрицательной волновой проводимостью. При использовании таких инверторов отрицательные проводимости суммируются с положительными проводимостями соседних линий.

Vv-il заииых на рис. В.(13.1в и г, это утверждение предполагает,

что [л/г|<:1. Указанное неравенство обычно выполняется на практике.

Многие другие схемы могут работать в качесгве инверторов сопротивлений нли проводимостей при условии, что нх характеристическое сопротивление будет веществеииым в рабочей полосе частот и их характеристический фазовый сдвиг будет равеи (±п/2)т, где m - нечетное число.

Для любого симметричного инвертора эти условия выполняются, если

№/2)ое= ~№/ )s<:.

(8.03.1)

где (XiJ2)oc - входное реактив,иое сопротивление разрезаиной ишолам цепи, когда проводники в плоскости разреза разомкнуты, а (:i,2)sc - сопротивление той же цепи, когда проводники в плоскости разреза закорочены.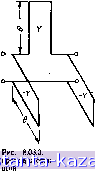

Инвертор состоя-иэ короткозанкну-тых шлейфов.

8.04. Использование частотного преобразования для перехода от прототипа нижних частот к полоенопропускающету фильтру

Характерчктлка прототипа ФНЧ, показанного а рис. 4.04.1, может быть точно связана с характеристикой соответствующего ППФ, показанного иа рис. 8.02.3, с помощью хорошо известного частотного преобразования

4 = -(--). (8.04.1)

где ю-относительная ширина полосы пропускания:

(8.04.2)

0)0=1 Wi<02 (8.04.3)

.Частоты ш' и и, относятся к характеристике ФНЧ, жак показано на рис. 8.02.1а, а частоты ш. шо, и ог - к характеристике соответствующего ППФ, как показано на рис. 8.02.16. Преобразование этого тнпа особенно полезно при определении требуемого числа резонаторов, необходимых для получения заданного затухания. Предположим, например, что требуется рассч1Итать фильтр типа рнс. 8.02.3 в звуковом диапазоне при величине пульсаций .чебышевской характеристики 1,0 дб в полосе частот от /i=2 кгц до 2=4 кгц и при затухании, по меньшей мере, 5066 иа частоте 1,5 кгц. Определим необходимое число резонаторов для получения нужной характеристики.

Из высажений (8.04.2) н (8.04.3) находим орносителыную ширину полосы пронусжания

4 = 0,707. Ис1польз\ем частотное преобразование (8.04.1)

тде fo = Ifzfi = 2,825 кгц, а частота, на которой затухание должно быть не меньше 50 дб, f=1.5 кгц. Тогда прототип ФНЧ долже-н иметь затухание, по крайней мере, 50 дб при отношении ш'/ш, , равном

=f-) =-1,914. Ц 0,707 2,В25 1.5 У

(Появление мшнуса объяоняется тем, что при математическом ттреобразовани-и часть характеристики ППФ, лежащая ниже частоты шо на рис. 8.02.16 будет соответствовать отрицательным 31на-чеииям частотной переменной и' для ФНЧ, в то же время характеристика ФНЧ, показанная на рис. 8.02.1а для отрицательных значений ш'. представляет зеркальное отражение характеристики для положительных ш'. В рассматриваемом inpwMepe 31наком минус можно преиебречь.

Используя график на рис. 4.03.46, ще были приведены чебышевские характеристики затухания фильтров с величиной пульсаций в полосе пропускания 1,0 дб, определяем, что ири чшсле реактивных элементов п=6 прототип будет иметь затухание .54,6 дб для отношения ш7ш; = 1,914 (т. е. -1=0,914), а

при п=б затуха.ние будет всего 43 дб. Таким, образом, для ППФ с полосой пропускания от fi=2 кгц до /2=4 кгц нео6.хх>димо п=6 резонаторов, чтобы обеспечить требуемое затухание на частоте f-1,5 кгц.

Характеристики тех фильтровых структур овч диапазона, котсь рые рассматриваются далее, очень хорошо совпадают при узких полосах пропускания с характеристикой фильтра на рис. 8.02.3, однако нх крутизна будет заметно отличаться от крутизны характеристики этого фильтра, если полоса пропу1скания увеличивается до 5% и-ли более.

.В данной главе в большинстве случаев будут использоваться приближенные преобразования, которые оказываются более точными для рассматриваемых структур, чем преобразование (8.04.1). Во многих случаях эти преобразования дают очень хорошие результаты даже для фильтров с полосой пропускан-ия до 20% или несколько больше. Хотя предла1гаемые функции преобразования несколько отличаются от преобразования (8.04.1), их точно та-- 374 -

КИМ же образом можно использовать для определения требуемого числа резонаторов, обеспечивающего выполнение зада.нных условий.

8.05. Фильтры из отрезков передающих линий, связанных ешкосгными зазорами

На рис. 8.05.1 Схематически изображен фильтр, который состоит из-связанных резонаторов, представляющих отрезки передающих линий полуволновой длины иа средней частоте шо с по-

рис. 8.05.1. Схематическое изображение фильтра из отрезков передающей линии, свнзанныч емкостными зазорами

следовательной емкостной связью между резонаторами. Расчетные формулы для таких фильтров приведены ниже.

Расчетные формулы для фильтров из отрезков передающей линии, связанных емкостными зазорами

(8.05.1) (8.05.2) (8.05.3).

I I

где Й, g,.....g опредыены на рис--M.l;

частота w показана на рнс. B.Ojlfl; ш - относительная ширина лолосы пронуокания; , /, J+J - пзращетры инверторов лровод1Шостеи;

Ес:;;;ГиГаГь%т\°а'17ви=;;Галь о

то реактивная проводимость этой неоднородности сомасно рис. 8.03.2г равна.

/.l+L l- +° (8.05.4).

где Bj j+i и Oj определяются на частоте (Оо.

Д,я KOHCipvKHHH. показакяо,-. иа рис 8.05.3d. по ..звестным значениям /j.it,/ с амощью графжов на рис. 8.05.20,о' сшреде1якггся зазоры Л; далее - 376 -

а) 1.0,

0.0S D,Oi

0.B3

Рис. 8.05.2. Графики оля расчета параметров У-инверторов. реализованных с помощью емкостных зазоров в полосковой линии с прямоугольным внутренним провпдником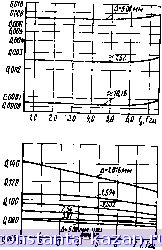

, L.paS/Fm

D/.(0,02096 Д-т). рад; Д -зазор т^мм; для Д<1 ям ч>=-Sarctg j,yt) Волновое соаро-тивледие передающих линий Zo= =* 50 бм; f, - средняя частота полосы пропускания. ггц

для пол^ченных значений Л по графикам на рис. 8.055в определяются параметры <\ i, j+t. Затем вьгчисляютсн мелтрическне длины

0/1;-!-- = + Y( + +)

Здесь величины ф/, /+) обьмно отрицательны.

Преобразование характеристики .прототипа ФНЧ в соответствующую ха-раитеристику ППФ может быть вЫПолнено с помощью лриблкжениой формулы

(8.05.7)

и' 2 -

Ю; -п>1 \ .

\ Щ + Щ J

Величины 01 и uj[ определены на рнс. 8.02.1а, рис. 8.02.16.

(8.05.8) (8.05.9)

а (О, Шо, <)1 и €02 - на

Для фильтра, показанного на рис. 8.05.1, используются инвер-горы, приведенные на рнс. 8.03.2г, которые обусловливают увеличение нагрузочнЫХ сопротивлений а коицах хаждого полуволнового резонатора, в результате чего, как можно показать, полуволновые резонаторы работают в режиме параллельного резонанса (см. § 8.14). Таким образом, эти фильтры работают подобно фильтрам с резонаторами параллельного типа, для которых общие расчетные формулы были приведены на стр. 369.

Еслн считать зазоры просто последовательными емкостями, то проводимости емкостных связей можно вычислить из выражений (8.05.1) -(8.05.4), а расстоя!ние в электрических jpaflycax между соседними емкостными неоднородностями - из выражения (8.05.5). Однако во м1иогих практических случаях емкостные зазоры между резонаторами оказываются настолько большими, что они йе могут быть представлены как простые последовательные емкости.

Рассмотрим, например, емкостный зазор в полосковой линии, показанной иа рнс. 8.05.3а. Еслн длина каждого резонатора определяется как расстояние от средней линии одного емкостного зазора до средней линии соседнего зазора (как показано ва рис. 8.05.1), то эквивалевгная схема зазора относительно его средней линии будет включать, кроме последовательной емкости, некоторую отрицательную парал- >

ЛеЛЬНуЮ емкость, появившуюся как резуль- Ь-расстояние между на.

тат уме.чьше ия параллельной емкости в лиТии? -д™

окрестности средней линии зазора. На рис. JIJJ т^х'же едииишх 8.05.36 показана такая эквивалентная схе- чт и величина ь ма зазора, а в подписи под рисунком приведены также некоторые соотношения, взятые из работы Олинера [9], который вывел приближенные выражения для определения реактивной проводимости в полосковой линии, имеющей почти нулевую толщину. Алышулер и Олинер [10] показали, что эти выражения обеспечивают приемлемую точность, если отноше.ние ю/б достаточно велико (больше 1,2). Это, например, имеет место в случае 50-омиой полосковой линии с почти нулевой толщиной и воздушным диэлектриком. Однако если отношение w/b мало, то ошибка будет значительной.

Получив достаточно точные значения проводимостей нз указанных выражений, можно вычислить соответствующие параметры инвертора проводимости для зазора с заданными размерами из - 377 -

Рис. 8.05.3. Эквивалентная схема зазора в по. лосковой линии.

-- [Чт)]

ь . Г