 |
 |
 |
 |
|
Главная -> Согласующие цепи 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 [ 65 ] 66 67 68 69 70 71 72 73 8.07. Узкополосиые фильтры из объемных резонаторов, связанных малыми диафрагиамя Расчет фильтров из объемных резонаторов, связанных малыми диафрагмами, может быть выполнен в самом общем виде с помощью теории малых апертур Бета (см. § 5.10). Для большин- 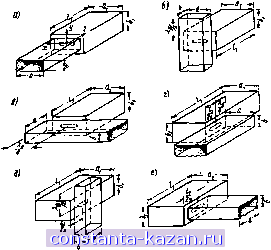 Рис. а07Л. Различные спосовы соединения прямоугольного резонатора с нагружающим волноводом. При связи с пожяцью малых днафрагы внешняя довротвостъ резонатора вычисляется из выраженнй: случае. н 6 --.г^. ДЛЯ случаи if <*,!*, na- f пя случая г для с. .я а к J- i : - ueiioe число ства фильтров, рассматриваемых в настоящей главе, расчет удобно проводить с использованием параметров крутизны резонаторов Vj- нли Ь] и параметров инверторов Kj,j+i или Jj,i+\. Однако в давном параграфе предпочтительнее использовать эквивалентный метод, который связан с понятиями внешних добротностей (Qe)A il (Qe)s каждого крайнего резонатора, имеющего свою нагрузку, II коэффициентов связн kj,j. между соседними резонаторами. Эти понятия были введены в § 8,02 и им соответствуют обобщенные соотношения (8.02.14)-(8.02.16) и (8.02.22) -(8.02.24). В подписи под рис. 8.07.1 приведены выражения для внешней добротности прямоугольного объемного резонатора, связанного различными способами с нагружающим волноводом. В этих выражениях, равно как и далее, приняты следующие обозначения: /. - длина волны в свободном пространстве; /.j и Лл-длины воли в волноводах: (8.07.1) i - число полуволн на длину d объемного резонатора; Ui - коэффициент магвитной поляризуемости диафрагмы, а величины а, Ь, at, 6i и k. являющиеся геометрическими размерами резонатора и нагружающего волновода, показаны на рисун-ках. После того как из выражений (8.02.14) и (8.02.15) или (8.02.22) н (8.02.23) определены значения добротностей (Qt)A и (QJb, с помощью соответствующего уравнения в подписи под рис. 8.07.1 может быть определено требуемое значение М,. Затем, используя рнс. 5.10.4 а, б, можно найти размеры диафрагм связи. Следует отметить, что величина Mi имеет размерность {еди-  с Рис. 8.07.2. Различные опособы соединения прямоугольных резонаторов. Если днвфрагыа мала, kdsi пт связи резонаторов вычисляется hj ажен] для случая а Ml Я' я lis -s - целое число для сл уч Alma длины)*, что согласуется с указанными уравнениями под рис. S.07.1 ,и с нормированием ординат на рнс. 5.10.1 а, б. В подписи под рис. 8.07.2 приведены выражения коэффициен-Юе связи к для двух прямоугольных резонаторов, связанных ма-Той диафрагмой в торцевой нлн боковой стенках. Обозначения аругих параметров в этнх выражениях совпадают с соответствующими обозначениями под рис. 8.07.1. Требуемые зиачення коэффициентов связи двух смежных резонаторов фнльтра могут быть вычислены с помощью выражения (ft.02.16) нли (8.02.24). Затем, пользуясь соответствующей формулой под рис. 8.07.2, определяют величину Ml для различных диафрагм связи. Точно так же, как и для оконечных диафрагм, размеры внутренних диафрагм определяются с помощыо рис. 5.10.4а, б. Дтя узкополосных фильтров, которые рассматриваются в данном параграфе, удовлетворительную точность должно дать частотное преобразование (8.07.2) где В качестве примера использования предлагаемого метода рассмотрим расчет трехрезонаториого фнльтра с епосредствеивыыи связями на волноводе WR=-90 ( =22,86 мм, 6=10.16 мм). имеющего в полосе пропускания величину пульсаций затухания 0,01 дб. Средняя частота полосы лропускання - 10 Ггц. Выберем ширину полосы пропускания 50 Мгц (ш=0,005) и длину ;i=?kgi/2= 19,85 m.u (s=l). Элементы прототипа ФНЧ определяются из табл. 4.05.2: ft=gi= 1,000; gi-gs=0,6291; g2=0,9702. На pnc. 8.07.3 показан эскиз этого фильтра. ¥\У \.У \у \. \у I Рпс. 8.07.3. Реализация узкополосного фильтра с непосредственной связью резонаторов малыми диафрагмами Из выражений на стр. 367 находим добротности {Qe)а={0.е)в = =g,(u;a= 125,8 н коэффициенты связи ka = ka=w\aiy gigi= = 0,0064. Используя далее рнс. 8.07.1а и 8.07.2а, определяем величину Ml для оконечных н внутренних диафрагм и получаем значения 108,49 и 12.95 соответственио. Для оконечных прямоугольных диафрагм выбираем отношение d2.rfi=0,5 (см. рнс. 8.07.3) и из рнс. 5.10.4а по кривой для прямоугольных диафрагм .находим первоначальное аначение dz= =8,738 мм. Однако сГг составляет значительную часть от длины волны >.= 3 см, поэтому, пользуясь выражением (5.10.3), определяем приближенную поправку и окончательно получаем dz= =7,874 мм; d,=3,937 .ил. inawerp внутренних круглых диафрагм находим из выражения d= I 6M. что дает 4,267 мм (см. § 5.10). Если толщина диафрагмы равна 0,12 мм или меньше, то поправка на толщину согласно выражевию (5.10.5) оказывается незначительной. Однако в случае большей толщины эта поправка должна быть учтена. Наличие диафрагм приводит к некоторому уменьшению резонансных частот резонаторов (по сравнению с отсутствием диафрагм). При желании можно осуществить небольшую коррекцию длины резонаторов с помощью выражений (8.06.5). В рассматриваемом примере нормированные реактивные со. противления Ху, j+i,Zo могут быть найдены из соответствующего выражения в табл. 5.10.1, которое для симметрично расположенных диафрагм на рис. 8.07.3 имеет вид (8.07.3) (i)/.l-fi /=.0.1.2,3 btlji где XmIZo и -Yji/Zo относятся к оконечным диафрагмам. Метод расчета в данном параграфе, основанный на теории ма-тых апертур Бета, ябляется весьма универсальным. Однако он иснсвываегся иа предположении, что диафрагмы связи достаточно малы, а это, в свою очередь, означает, что относительная ширина полосы пропускания фильтра w также мала, (например, порядка 0,01 нли меньше). Вывод выражений, приведенных а подписях под рис. 8.07.1 и 8.07.2, изложен в § 8.14. 8.08. Фильтры, использующие четвертьволновые резонаторы (включенные как четырехполюсники) В ф.чльтрах, рассмотренных в § 8.05, используются полувоЛ|НО-вые резонаторы и /-инверторы типа, представленного на рнс. 8.03.2г. Соотношения для их расчета могут быть получены лз формул, приведенных на стр. .369, как это будет показано в § 8.14. В фильтрах, рассмотренных в § 8.06, используются полуволновые резонаторы и /<-1шверторы типа, представлениого ,на рис, Ь.03.1 в, а их расчетные формулы могут быть получены <из обобщенных соотвошеннй на стр. 367. Если аналогичным образом используются четвертьволновые резонаторы, то они сами будут эб-ладать инверториыми свойства.мн. Так, что когда с одного конца каждый резонатор ведет себя как резонатор последовательного ти-- 393 - па (см. рис. 8.02.5J, то с другого конца он действует как резонатор параллельного гина (см. рис. 8.02.6). Таким образом, нетрудно показать, что фильтры могут быть выполнены нз четвертьволновых резонаторов, включенных как четырехполюсники, если они соединяются поочередно К- и /-инверторами [14]. а By, Рис. 8.08.1. Ох&матическое изображение фильтра с четвертьволновыми резонаторами, включенными каж четырелпол юсн нки  На рис. 8.08.1 приведено схематическое изображение фильтра С колебаниями типа ТЕМ, в котором используются четвертьволновые резонаторы с чередующимися J- н /(-инверторами, соответствующими емкостному зазору и параллельной индуктивности. Ниже приведены формулы для его .расчета. РАСЧЕТНЫЕ ФОРМУЛЙ ДЛЯ ФИЛЬТРОВ С ЧЕТВЕРТЬВОЛНОВЫМИ РЕЗОНАТОРАМИ. ВКЛЮЧЕННЫМИ КАК ЧЕТЫРЕХПОЛЮСНИКИ К 01 / 4(0, Veigf+i (8.08.1) (8.08.2) (8.08.3) где go. 1.....gn опредепены на рпс. 4.04.1, a wj -на рнс. 8.02.1(7; w - относительная ширина лолосы .прооруоьання, определяемая ниже. В этой стр>жтуре инверторы сопротивлений .(с параметрами Kj, чередуются с инверторами .проводимостей (с .параметрами j+i); 2о= - - волновое сопротивление линии между инверторами, о При испо1ьзовапин /fj, j+i инверторов сопротивлений и ,-+1 инверторов Гводнмостей, .показанных соответственно на рис. 8.03.1в н 8.03.2г. вел1гчины i. J+1 фл, i+i можно определить по форм-улам приведенным в .под-онсял ж эпш рнсункйм. Тогда 1/ = +1-(т,-1.,--1-?,-./+1). POS. где фй. k+i - отрицательны. (8.08.4) 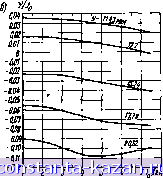  |
|
© 2025 Constanta-Kazan.ru
Тел: 8(843)265-47-53, 8(843)265-47-52, Факс: 8(843)211-02-95 |