где 01 определено ниже. Емкости с&№1[ равны:

п п+1 - 1/ г

Параллельные емкости равны:

Ci - - Cgl - Cia;

с„=с-с„ -с;.

(8.11.2) (8.11.3) (8.11.4)

(8.11.5)

(8.11.6) (8 1! 7)

(8.11,8) (8.11.9)

(8.11.10)

где величины Cj,j+i определяются с помощью ф-л 1(8Л1.5)-*(8.11.7), а емкости Ср, и С^ из следующих двух выражений:

С.., 4-.

(8.11.11)

(8.11.12)

Если mz/toii,05. То Приближенное преобразование частотной харажтери-СТИ1КН прототипа ФИЧ в характеристику ППф выполняется ino -формуле

(8.11.13)

в

- 408 -

(8.11.14) (8.11.15)

В случае ш../М1>1.ио соответствующее частотное преобраЭоиан[1е и опре енне ,1 (,1и недуе, выполнять, как указано ниже, на стр. 411.

РАСЧЕТНЫЕ ФОРМУЛЫ ДЛЯ ФИЛЬТРОВ НА СОСРЕДОТОЧШНЫХ ЭЛЕМЕНТАХ С ИНДУКТИВНОЙ СВЯЗЬЮ

(Зпретеление велнчггн gj, (nj, шо, ьп, соа и УС j+i осуществляется с пофющью рис. 1.04.1, 8.02.1 и 8.03.1о.

riocie выбора зна-ieHiHi Ra, Ra, Lrc, L,i, L,n и L n+i, гле индуктивности Lrj снизаны с Lp прнведенныМи ниже выраженнял^п (8.11.30)-.(8.11.34). опретеляютсч нел№11шы.

с„,=,+ = у4г; (8-11.16)

goS.o>l

(8.11.17)

i.;-Hl;-l -l= ы,

l/zibl+l; (8.11.18)

1 У eisi+i

К.п^\ = /--

де naioci <с о.преде1е[[а ниже.

Коэффициенты вза|[моииду1ШИ11 равны:

(8.11.19)

(8.11.20) (8.11.21) (8.11.22)

Пос1елаБаге.1ьные HHflydiTHBHoCTH для схемы на рис. 8.11.26 равны:

K = Ln-M ; (8.11.23)

1-1 = 11- Чщ - .И ; (8 11 24)

i/, , = iW-Al,.M -Al (8.11.25)

in=im-Л' 1, -HJ.,., . (8.11.26)

= >1+1~л,п-И, (8.11.27)

Л)о1 -I-

C-ro-AMl/Hoif.,

(8. II.28)

Л< . +1+--

(8.11.29)

Для с.\емы ка рнс 8.11.2й лшные индуктивности Lpj контуров равны;

l- = Lro: (8 4.30)

Lpi = tri + Л^О! - ; (8.11.31)

Pf, -1 = , <8-11-32)

-,=,n + м„,n+i-K.n+. (8.11.33)

..+. = -...+1. (84-34)

Если Wi/coi!l,05, то приближенное прео6разоваН1ге частотной характери-СТ1ЖИ прототипа ФНЧ в характеристику ППФ выполняетсц по формуле

(8.1!.35)

(8 11.36)

(8.11.37)

В случае m2/c)i>l,05 соответствующее частотное преобразование и определение ш и Шо выполняются, как указано ниже, на стр. 411.

В структуре с сосредоточенными параметрами, приведенной иа рис. 8.1 l!l, применяются резонаторы параллельного типа с реактивной проводимостью Bj((i)) и /-инверторы типа, показанного на рис. 8,03.26. Эта структура соответствует схеме на рис. 8.02.6.

На рис. 8.11.1 представлены эффективные емкости Cj, которые используются для ошределения резонансной частоты и параметров крутизны реактивной проводимости резонаторов. Но параллельные емкости, .используемые в схеме, будут меньше чем Ctj, что видно из выражений (8.11.8) -(8.11.10). Это объясняется тем, что для определення полной параллельной емкости, действительно включаемой в схему, требуется вычесть из положительной емкости резонатора отрицательную емкость инвертора.

.Оконечные емкости связи Coi н C ,n+i определяются несколько иным способом (см. § 8.14) для того, чтобы не пришлось иметь дело с отрицательными емкостями перед нагрузками Од и Ge. Отметим, что велич|ины Сл, Ов и Cj могут .иметь .любые требуемые значеяия.

Схема на рис. 8.11.26 будет точно дуальной схеме на рис. 8.11.1, если и.ндукти.В1Иости iro и Lr, п+1 выбрать равными соответственно Л1о1 и Мп, 71-и, что приведет ж соотношению Lo=Ln+i=0. Расчетные ф-лы (8.11.16) - (8.11.37) несколько вищоизмеиены по сравнению с ф-лами (8.11.1)-(8.11.15) с тем, чтобы их легче можно было использовать для схемы, показанной на рис. 8.11.2а. 16* - 410 -

Частотное преобразование, приведенное иа стр. 408 (сч, расчетные формулы данного параграфа), будет точным только в случае узких полос пропускания. Коном [1] доказано, что приближенное частотное преобразование

2- - о>1

где

Юо = Ci)i -(- со,- /(mz-(i)i) +

Cl)iCl)2,

(8.11.38)

(8.11.39)

дает хорошие результаты для относительной ширины лолосы лро-пускания до 20%. В этом слуиае величина w определяется из выражения (1])

(8.11.40)

8.12. Полосиопропускающие фильтры с широкими полосами , запирания [16]

У всех рассмотренных до сих пор фильтровых структур из отрезков передающих линий имелись дополнительные полосы пропускания на частотах, кратных частотам первой полосы пропускания или, в крайнем случае, представляющих нечетные кратные этих частот.

На рис. 8.12.1 показана фильтровая структура, которая при соответствующем расчете может ие иметь паразитных .полос про-

Рис 812.1. Схематическое изображение пшоснопропус-кающего фильтра с широкими полосами запирания

) Приведенное здесь выражение для w отличается от выражения для о/, использованного Коном (J], на множитель шо/ш,. Это учтено в наших расчетных формулах и они дают правильный конечный результат. Ве.пичкна w в выражении (8.Г1.40) представляет собой относительную ширину полосы пропускание, в то время как величина и/, введенная Коном, таковой не является.

Яуокания вплоть до очень высоких частот. Ниже тривеаены формулы для ее расчета.

РАСЧЕТНЫЕ ФОРМУЛЫ ДЛЯ ПОЛОСНОПРОПУСКАЮЩИХ ФИЛЬТРОВ с ШИРОКИМИ ПОЛОСАМИ ЗАПИРАНИЯ

Олределенне вё.-111Чин g/, m, шо, tui, шв и Jjj+i осуществляются с помощыо рнс. 4.04.1, 8.02.1, 8.02.6 и 8.03.26.

После выбора значений Ол, Gh и Уо определяются (точнее оцениваются) величины:

7-- -I- т„с{ Н- (4,Ci2

тоС„ 1. + твС' +-

(8.12.1)

(8.12.2) (8.12.3)

веденного

ояются параметры А, a+i:

По .полученным значениям В^. Ко с помощью рнс. 8.12.20 или 6 либо прн-нного ниже выражения (8.12.16) определяются параметры Зс-тем вычмс-A+i:

,= l/-; (8.12.4)

gogl L

s.n-l-l =

(8.125) (8.12.6)

где w опредечяется no приведенной ниже ф-ле (8.12.11):

овання характер:

(8.12.7)

(8.12.8) (8.12.9)

Для приближенного преобразования характеристики ФНЧ в характеристику ППФ используется выражение

иг и

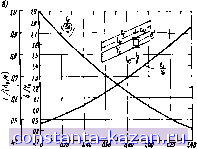Рнс. 8.12.2. Графики длн расчета резонаторов, обеспечивающих подавление паразитных полос пропускания вблизи частоты Зоо {о.) и 5шо {щ

=2():

(8.12.11) (8.12.12)

Параллельные емкости Cj в схеме, приведенной иа рис. 8.12.1, ие требуются для ее работы, а являются паразитными и обычно связаны с емкостями связи С/ ч-1.