Е -амплитуда напряжения, переданного в нагрузку (т. е. напряжения, которое может быть измерено на зажимах 2-2).

Если Z,=Zu то отражения не будет') и тогда Ег=0 и £,=£. Заменив четырехполюсник и генератор на рис. 2.08.1а эквивалевт-Hbiivi генератором, как показано на рис. 2.08.16, легко видеть, что так как Zs=Zi, и Ei=E, то

(2.08.2)

где for - напряжение, которое может быть измерено на зажимах 2-2, когда они разомкнуты. Используя ур-ния (2.08.1) и (2.08.2), можно определить коэффициент отражения по напряжению:

(2.08.3)

2

£, Ч +Z

При аналогкчном рассмотрении волн тока

/, + /, = /. (2.08.4)

где li - амплитуда падающей волны тока; /г -амплитуда отраженной волны тока:

/ -амплитуда тока, переданного в нагрузку (т. е. тока, фактически протекающего через зажимы 2-2). .Амплитуда падающей волны тока равна

/,= /,с/2, (2.08.5)

где /sc - ток, который проходил бы через зажимы 2-2, если бы они были замкнуты накоротко. Коэффициент отражения по току определяется как

(2.08.6)

где r.-.l/ZsH 1т,= 1/2.

Иногда используют коэффициент передачи напряжения

£, Ч +Ч

Соответствующий коэффициент передачи тока равен

(2.08.7)

(2.08.8)

Следует заметить, что коэффициенты передачи т и Тс отличаются от коэффициента передачи t, который рассматривается в § 2.10.

*) Заметш!, что отсутствие отражения волиы няпряжеиия не обязательно означает передачу максимальной мощности. При отоутствпн отражения Z = Zi., а передача максимальной лющности будет при Zg~Zj , где - величина. ко.чплексно-сопряженная с Zt,.

2.09. Определение входного сопротивления нагруженного четырехполюсника

Входное сопротивление четыремполюсника (Z( ), (рис. 2.09.1) может быть выражено через его нагрузку и любые параметры.

Рис. 2.09.1. К определению входных сопротивлений четы-pexпoлюcниJ{a

Используя либо обобщенные параметры, либо параметры холостого хода или короткого замыкания, можно получить следующие выражения:

(Z, )i = 2u-

(2.09.1) (2.09.2) (2.09.3)

(г^\----.

где 2=1/22. Аналогичные выражения получаются и для сопротивления (Z( )2:

(Z, ).= Z2,--

где У, = 1/2,.

(2.09.4) (2.09.5) (2.09.6)

2.10. Определение функций передачи напряжения

Функция передачи £g/£2 для цепи а рис. 2.10.1 может быть выражена через любые параметры четырехполюсника. Соответствующие равенства приведены ниже:

Eg AR.i-B + CRiR, Pj?i

£ - Ri).г^R,)-z,л, .

Eg (yu Ol) (Ум + Ог) - УгаУ.!

-y Gi

- 43 -

(2.10.1) (2.10.2) (2.10.3)

Рис. 2.10.1. К определению функций передачи напряжения. 0,=1/Я,; 0.-1/Я,

Функция передачи Ед/Ег, хотя и используется обычно, однако имеет определенный недостаток. Он заключается в том, что в зависимости от отношения величин сопротивлений Ri и Ri полная передача энергии может соответствовать любому из оче ь широкого диапазоша значений велич.нны [Eg/El. Этот недостаток можно устранить, если вместо указанной попользовать другую функцию передачи напряжения:

£L = L l/Z (2.10.4)

£j, 2 V Rl Ег

Величина

2 I

(2.10.5)

определяется здесь как номинальное напряжение, т. е. иапряже-пие, которое будет на сопротивлении Ra, если ноглощаеман н нем мощность равна максимальной (или номинальной) мощности генератора. Таким образом, при полной передаче энергии £j/£2 = = 1 независимо от отношения велич™ сопротивлений Ri и R2-След\ет отметить, что имеет ту же фазу, что и £2-

В литературе обычно используется рабочий коэффициент передачи напряжения

(2.10.6)

Этот коэффициент отличается от коэффициентов передачи т, Тг-которые были рассмотрены в § 2.08, и совпадает с коэффициентами матрицы рассеяния 5,2=52, (см. § 2.12). Следует отметить, что t является коэффициентом усиления напряження, т. е. представляет собой отношение напряжения на выходе к напряжению на входе, тогда как функция (2.10.4) является коэффициентом ослабления напряжения, т. е. представляет собой отношение напряжения на входе к .напряжению .на выходе.

2.11. Определение функций передачи мощности н затухания

Одним .из обычно используемых типов функции передачи мощности является функция вносимого изменения по мощ.ности, определяемая выражением

(2.11.1)

где R Ri, Eg и £2 показаны на рис. 2.10.1, а величина £g/£2 может быть вычислена с помощью ур-иий (2.10.1)-(2.10.3). Величина Р2 - мощность, потребляемая сопротивлением Ri, когда между ним и генератором включен четырехполюсник, а Р20 - мощность, .потребляемая сопротивлением Ri, когда оно подключено непосредственно к генератору Eg с сопротивлением Ri (т. е. когда четыре.хполюсник устранен).

Функция вноси-мого изменения по мощности, или, как ее еще часто называют, функция вносимых потерь обладает тем же недостатком, что и функция £g/£2, рассм.отренная в § 2-10, т. е. полная передача мощности может соответствовать почти любому значению велтииы P20IP2 в зави.с.имости от отношения сопротивлений R- н R2- По этой причине в книге будет использована другая функция передачи мощности:

(2.11.2)

Рт Р2

называемая обычно рабочим коэффициентом потерь мощ.ности-Здесь Р2 является мощностью, подводимой к сопротивлению R2 на рис. 2.10.1, а

(2.11.3)

- максимальная мощность генератора Eg с внутреяним сопротивлением R,. Такпч образом, три полной передаче мощности Рт/Р2= I независимо от отношения сопротивлений R, и R2. Заме-Т11, . что велич.нна t в правой части выражения (2.11.2) есть не что иное, как рабочий коэффициент передачи напряжения, опре-дсляе.чый соотношеиием (2.10.6).

Часто бывает удобно выразить рабочий коэффициент потерь .мощности в децибелах:

La = lOlg дб.

(2.11.4)

Выразпв теперь в децибелах и функцию вносимых потерь, используя сбозначенне i(= lOlgРго/Рг, получим:

LaL, lOlg , дб.

(2.11.5)

Заметим, что при R, = R2 рабочие и вносимые потерн одинаковы.

Обычно величину Lj. называют рабочим затуханием, а £( - вносимым затуханием. Однако в .книге для краткости будет использован термин затухание, под которым, когда это не оговорено особо, всюду будет пониматься рабочее затухание.

Если четыре.хполюсник на рис. 2.II.I содержит диссинативные элементы, которыми нельзя пренебречь, то затухание Ел может - 4.5 -

быть вычислено с помощью выражений (2.11.4) и (2.11.2) и любого риз ур-ний (2.ЮЛ)-(2.10.3). Однако, считая четырехполюсник чисто реактивным (т. е. без диссипативных элементов) можно воспользоваться некоторыми упрощениями. Например, как пока-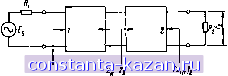

Рис. 2.il,l.l. К

нию коаффнЕИента передачи мощ-

ности для реаясгивиой цепи

зано в § 2.05, для ,цепи без потерь параметры А а D будут чисто вещественными, а В и С - чисто мнимыми для частот io). Поэтому при вычислениях удобно использовать выражение

(2.11.6)

Оно справедливо как для взаимных, так и для невзаим!ных четырехполюсников без потерь при передаче слева направо.

Если принять, что /?1=./?2=Л и, кроме того, что четырехполюс-.ник является взаимным (ЛД-ВС=1) и симметричным (Л = Д). то выражение (2.М.6) упрощается:

(2.11.7)

Если воспользоваться теперь обобщенными параметрами Л', В', С, D только для левой половины четырехполюсника, то с помощью (2.05.7) выражение (2.ill.7) для рабочего коэффициента потерь мощности всего четырехполкусника можно преобразовать к виду

в случае такого четырехполюсника без потерь передачу мощности легко рассчитать, зная (параметры генератора и входное со-противленне четырехполюсника, нагруженного на сопротивление Rl. Это объясняется тем, что мощность, поступающая в сопротивление (Zin)i, должна полностью поглощаться в нагрузке. Вычисления наиболее просто выполняются с помощью коэффициента отражения Г, рассмотренного в § 2.08. В этом случае

(2.11.11)

Коэффициент отражения со стороны выхода четырехполюсника равен

причем для четырехполюсника без потерь

Г, = Г=, (2.11.12)

так что в выражении (2.М.9) может быть использовано абсолютное значение любого из этих коэффициентов. Следует, однако, помнить, что фазы коэффициентов Г, и Гг в общем случае ие равны, даже если условие (2jMj12) вЫполняется. Коэффициент отражения

между Z и Zb (см. рнс. 2.11.1 раженни (2.11.9), ее можно показать, что

ri=rd=

(2.11.13)

Zj + Zo

раженни (2.11.9), есл.и 2 и Д - комплексные величины. Однако

моясет быть использован в вы-

<2.П.14)

где -величина, компленсно-сопряженная с Z. Таким образом, если Z =Ra+\Xa и Zb=Rb + \Xb, то с помощью выражений (2.11.14) и (2.11.9) получаем

Рт + № + (2 1115)

В тех случаях, когда Z =Zi например, для середины симметричного четырехполюсника, выра-жение (2..11.15) упрощается:

(2.11.16)

Другим случаем, который обычно встречается в фильтровых цепях, является четырехполюсник антиметричной') структуры. Если Z н Zj, относятся к середине антиметричного четырежполюс-яика, то для всех частот

1 = 1 + 1]

Pi \rJ

(2.11.17)

где Rh - некоторая вещественная положительная постоянная, имеющая размерность сопротивления. Принимая снова 2 =

) Этот тер.\п1н был введен Гиллемином (сы работу [2], стр. 371 и 476). - 47 -