частоту. В нашем случае ширина полосы пропус-кан'ИЯ была довольно большой, в связи с чем .метод попеременното короткого замьжания и холостого хода ие дал полностью удовлетворитель- \. ных результатов, что под-Ш Ш 1,50 155 игц .рврржда^ось некоторой несимметричностью характеристики IB полосе пропускания. Однако, как было затем установлено, это оказалось .возможным легко исправить с помощью подстроечных винтов оконечных резонаторов'), применив генератор качающейся частоты н рефлектометр с самописцем. .После настройки фильтра были измерены ков на входе и затухание. Эти данные приведены на рис. 8.13,4.

Характеристика ков на рис. 8.13.4а приблизительно соответствует чебышевской характеристике, но с пульсацией 0,2 дб вместо 0,1 дб. По-видимому, это .расхождение вызвано тем. что в расчетных формулах для гребенчатых фильтров (см, стр. 420 и 421) не учитывалась связь между резонаторами, не являющимися соседними. Меньший уровень пульсации можно получить регулировкой зазоров Soi и между входной линией и .первым резонатором и между четвертым резонатором и выходной линией. Аналогичное явление наблюдалось и .в фильтре на встречных стержнях, который рассматривается в § 10.06. Уровень пульсаций в полосе про-

*) При иопо-тьзованни указанного метода (см. § 1.1.05) именно оконечные резонаторы обычно вызывают трудности при настройке, так как нх связи совершенно отличаются От связен внутренних резонаторов.

- 436 -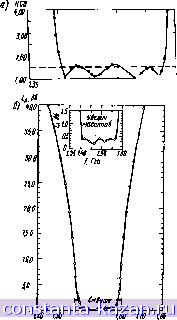

<*7 (50 Г.Ггц

Рис, 8.13.4. Экопернмектальные характеристики фильтра, покаэаннсм-о на рнс. 8.13.3: а- ксв; б - затухание (.первая паразитная полоса ва частоте 6,3 Ггц)

пускания в этом фильтре был легко снижен путем уменьшения оконечных зазоров So\ н 5 , п-м- В то же время уровень пульсаций, отмеченный в характеристике на рис. 8.13.4а, ше настолько превышает допустимые значения, чтобы стоило затрачивать время на дополнительные астройкн.

Из.меренная по характеристике ксв на рис. 8.13.4а отнооитель-пая ширина полосы пропускания иа уровне одинаковых значении пульсаций ксв оказалась равной ю = 0,116 вместо заданной 0,1. Увеличение ширины полосы пропускания может быть также объяснено влиянием связи между резонаторами, не являющимися соседними, которое не было учтено .при выводе указанных расчетных формул.

В табл. 8.13.2 сравнивается затухание, вычисленное с помощью преобразовании (8!l3.8)-(8,13..10). и измеренное затухание. Условия А относятся к .первоначально заданиы'М параметрам, а. условия Б соответствуют ширине полосы пропускания ш=0,116 и пульсации, приблизительно равной 0,2 дб (см. рис. 8.13.4а),

ТАБЛИЦА 8.13.2

СРАВНИТЕЛЬНАЯ ТАБЛИЦА SATJX.AIHin. ПОЛУЧЕННЫХ С ПОМОЩЬЮ ЧАСТОТНОГО ПРЕОБРАЗОВАНИЯ II НЗ.ЧЕРЕННЫХ

Следует заметить, что .по изложенным ранее причинам, в любом случае, затухание, определяемое .преобразованием для = 1,25 Ггц (/<ifo). б.тиже ж исти-иному, в то время как затухание, определяемое преобразованнем для t=\J Ггц, (/>/о) несколько ниже.

8.14. Вывод некоторых расчетных соотношений

При изложении ..материала в .предыдущих параграфах, для удобства пользования им при'.практических расчетах фильтров, были опущены некоторые теоретические вопросы. Они .рассматриваются в настоящем параграфе.

Вначале покажем, как выводятся расчетные соотношения для случая обобщенной структуры лз связанных .последовательных .резонаторов, приведенной на рис, 8.02.5.

Каи следует из § 4.12, прототио с сосредоточенными параметрами и представленный а рнс. 8.02.2, ожет Йыть преобразован в схему, приведенную на р-ис. 4.12.2а (где значения Ra, и Непроизвольны),.причем характеристика передачи останется той же самой. От этой йизкочастотной схемы можно .перейти к соответствующей полоснопропускающей схеме с сосредоточенными пара-метрами, используя частотное преобразование

где

(8.14.1)

(8.14.2)

1ао = ) ш^, (8.14.3)

а ю', ш ш, то, coi и сог показаны на рис. 8.02.1 для чебышевски-х фильтров. Тогда последовательные реактивные сопротивления и приведенные на рис. 4,12.2а, преобразуются следующим об-рйЗом;

где

С = -

(8.14.4) (8.14.5)

(8.14.6)

Эти же рассуждения справедливы и для преобразования низкочастотной схем.ы а рис. 4.12.2а непосредственно в полоонопропус-кающую схему, .представлениую на рис. 8.02.4, Чтобы вывести интересующие нас общие расчетные соотношения (см. стр. 367), используем .виача.пе функцию

X;(o)) = L <o-(8.14.7)

для реактивных сопротивлений резонаторов в указанной схеме, необходимую для определения параметров крутизны резонаторов:

Затем с помощью выражений (8.14.6) ai (8.14.8) пюлучим

i =- (8.14.9)

I - 428 -

Подставляя этот результат в выражения, приведенные в подписи под рис. 4.12.2а, получае.м ф-лы (8.02,10)-(8.02.12).

Формулы (8.02,14) и (8.02.15) получаются .с помощью выражения (8.14.8), рис. 4.12.1 и выражения для внешней добротности Qe окоиечиых резонаторов, которое яредставлмт собой величину coori или шогп, деленную иа соответствующее, преобразованное оконечным инвертором, активное сопротивление нагрузки.

Формула (8.02.16) может быть получена в результате замены на рис. 8.02.4 деалиэнрованных инверторов сопротивлений инверторами, схема которых показана на рнс. 8.03.1О. Новая схема окажется аналогичной схеме иа рис. 8.11.26, которая эквивалентна цепи с трансформаторной связью, приведенной на рис. 8.11.2а. Тогда каэфф .циенты свйэи для внутренних резонаторов фильтра будут равны

i. 1+1

(8.1410)

Формула (8.02.16) является более общей по сравнению с этим выражением. Так, например, для схемы яа рнс. 8.11.2 Kj,i+t = = ci)djMj, i+i и Xj=aQLpj. Если, эти величины подставить в выражение (8.14.10), то получим указанное соотношение (8.02.16).

Расчетные формулы на стр. 369 можно вывести совершенно аналогично из рис. 4.12.26, -используя свойства дуальных схем. Выражения для параметров К- и /-инверторов в случае различных фильтровых структур, рассмотреннык в этой главе, получаются в основном путем вычисления параметров крутизны х нлн b для данной структуры резонатора с последующей подстановкой их в формулы, приведенные на стр. 367 или на стр. 369. Таким обра-30.Ч, выводы всех расчетных выражений для различных типов фильтров, рассмотренных в настоящей главе, основываются в значительной мере на общих расчетных формулах, приведенных в § 8.02.

.фильтры с емкостной связью (см. § 8.05). Выведем соотно.шеиия для .параметров крутизны реактивной проводимости резонаторов для .фильтра, представленного на рнс. 8.05.1 и состоящего из отрез.ков передающие линий, связанных емкостны.адн зазорами. В этом случае длина .резонаторных линий приблизительно равиа половине длины воЛ1ИЫ на средней частоте полосы пропус-.кания, и еслн резонатор нагружен на сопротивление Zt, то в.ход-ное сопротивление этой линии определяется выражением

пли (для 10, близких h ыо)

2o + lZi.

(8.14.12)

В случае узкой или умеренной полосы пропускания фильтры того же типа будут иметь относительно малые емкости связи. Следовательно, можно показать, что на концах каждого резонатора бу-.дет относительно высокое сопротивление. Используя это условие, т. е. Zi.>Zo. в выражении (8.14.12), получаем, что, ло крайней мере, на частотах вблизи юо указанное .выражение сводится к более простому

., (8.14.13)

1-.-1-1 в (о)

(8.14.14) (8.14.15)

Таким образом, выражение для входного сопротивления Z,- линии аналогично выражению для .параллельного соединения проводимости нагрузки Yl и реактивной проводимости резонатора В(ю).

Используя ф-лу (8.02.17) из соотношения (8.14.14) получаем выражение для параметра крутизны реакти-вн.ой проводимости ]-\Го резонатора:

(8.14.16)

Так как волновая проводимость Yo всех линий на рис. 8.05.1 одинакова, то все .параметры ирутизиы Ь также равны. Подставив выражение (8.14.16) в ф-лы (8.02.18) -(8.02.20), получим ф-лы (8.05.1) -(8.05.3). Интересно отметить, что фильтр, показанный на рнс. 8.05.1, может быть выполвон из резонаторов, длина которых составляет и полуволн на средней частоте во требуемой полосы иронускан-ия. Прн этом параметр крутизны, реактивно.* проводимости определяется из выражения

6/ = 5.. (8.14,17)

.Волноводные фильтры (см. § 8.06). Волноводныйфильтр, представленный на рис. 8.06.1, с параллельными индуктивными связями дуален фильтру с последовательными емкостными зазорами, приведенному на рис. 8.05,1, за исключением одного важ-- 430 - >

ного отличия. Это отлнчие заключается в том, что в волновод-ном фильтре должно быть учтено изменение дл.1шы волны в волноводе kg из-за дисперсии. .Можно .показать, что если характеристика волноводного фильтра построена в за.виснмости от переменной \lkg вместо частотной переменной ю, то она будет иметь тот же самый вид, что н характеристика эквивалентного полоскового фильтра на рис. 8.05.1,

Таким образом, вы.ражения на стр. 383 будут просто дуальны выражениям на стр. 375 н 376, если отношения частот ш/юо, mi/mo и ыг/ша заменить соответствующими отиошениями длин волн в волноводе sol-e, Лда/XsL и kgolkgi, .Где kga-длина волны в волноводе в середине полосы пропускания. Полуволновые резонаторы в этом случае имеют резонанс .последовательного типа с параметром крутизны

Xi = -jZo. (8.14.18а)

Выражение (8.14.18а) применимо к воляоводным резонаторам только тогда, когда частотная переменная заменена переменной l/kg (или kgalkg). Однако для резонаторов с волнами типа ТЕМ указа-иное выражение применяется .как при частотной .переменной, так и при переменной l/?.g.

Если в волноводном фильтре в качестве частотной переменной используется круговая частота ш, то параметр крутизны следует вычислять с учетом дополнительной зависимости kg от частоты. Прн этом согласно § 5.08 параметр офутизны определяется из со-онношения

(8.14.186)

.в конкретном расчете фильтра различие между параметрами крутизны, вычисленными нз соотношений (8.14.183) и (8.14.186), ком.пенсируется тем, что относительная ширина полосы пропускания W, выраженная через частоту, йудет отличаться от относительной ширины полосы пропускания шх-, выраженной через длину волны в волноводе, на коэффициент (kgolkoY. по крайней мере, для уэкополосных фильтров [см. ф-лу (8.06.7)]. Для большинства волноводных фильтров удобнее пользоваться переменной kgolkg, хотя может быть использована и частотная леременная.

Подставляя выражение (8.14.18а), величины Ка=Кв=о и а' (вместо ш) в ф-лы (8.02.10)(8.02.12), получаем ф-лы (8.06.1)- (8.06.3).

УзкоиОлосные фильтры из объемных ,pe3o.iia-торов (см. § 8.07). Вывод расчетных формул, приведенных в § 8.07. рассмотрим пользуясь схемой на рис. 8.07.1а. На этой схеме показан объемный резонатор, который связан небольшой диафрагмой, имеющей коэффициент магнитной поляризуемости Л!., с прямоугольным волноводом с колебаниями типа ТЕю (см. § 5.10). Составляющие электрического и магнитного полей в объемном - 431 -