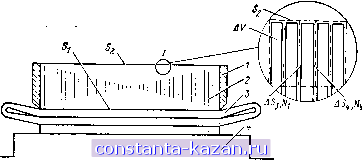Рис. 2.3. Конструктивная схема ферромагнитного экрана с нажимными

плитами:

J - нажимная плита; г - ферромагнитный экран; 5 - обмотка якоря; 4 -ротор со сверхпроводниковой обмоткой возбуждения

Указанные особенности приводят к необходимости больпюго числа разбиений п при численном интегрировании по (2.25). В качестве иллюстрации рассмотрим некоторые итоги численного интегрирования по (2.25) ядра интегрального уравнения (2.20) в предположении, что плотность поверхностных магнитных зарядов на внутренней и наружной поверхностях ферромагнитного экрана . равномерно распределена по длине машины и синусоидальна. Численное интегрирование проводилось по формуле Ньютона-Котеса восьмого порядка.

Допустим, что точка X,- находится на поверхности Sk {кфЧ), по которой выполняется интегрирование. Как показали серии расчетов с различными размерами поверхности Sk, погрешность численного интегрирования в среднем около 1% достигается при числе разбиений п л; 104-10*. Например, в случае криогенного генератора мощностью 200 кВт (рис. 2.4) для численного интегрирования в точке Xi с погрешностью до 1% потребовалось около 40 000 разбиений поверхности Si.

При численном интегрировании по формуле (2.25) в точке XiSk по поверхности 5,- {кФ1) для получения погрешности 1% требуется nalO-lO разбиений поверхности Si. В этом случае число разбиений я зависит от расстояния между точкой X, и поверхностью S/. В том же генераторе мощностью 200 кВт при численном интегрировании с указанной погрешностью в точке Хг потребовалось около 4000 разбиений поверхности S\-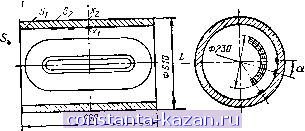

Рис. 2.4. Конструкция и размеры статической модели криотурбогеиератора

Таким образом, если замена интеграла конечной суммой проводится по формуле (2.25), то из-за слабой особенности в ядрах интегральных уравнений (2.20) и (2.21) приходится решать систему линейных уравнений порядка 103 10*. Чтобы уменьшить порядок системы линейных уравнений, численное интегрирование целесообразно проводить, разбивая область D на я элементов AD и считая плотность магнитных зарядов в AD постоянной. В этом случае интеграл заменяется конечной суммой по формуле [2.4]

п

[K{Xi, x)Y{x)dx SУ(t) \ K{Xi,x)dxR{K{xi,x)Y(x)\.

г ; 1 А г

. (2.27)

при расчете по (2.27) точность замены интеграла конечной суммой зависит от точности интегрирования функции плотности магнитных зарядов, что в 10-100 раз уменьшает порядок систем линейных алгебраических уравнений. Интеграл по области D вычисляют, используя адаптивную программу численного интегрирования. Коэффициенты системы линейных алгебраических уравнений, аппроксимирующей интегральное уравнение (2.10), имеют значения

at; =

A{Xi)-X S/*C(Xb x)dx; ij;

\K{Xi, x)dx;

(2.28)

В интегральных уравнениях (2.20) и (2.21) Л(х)=1 и

[KiXi, >c)dx:0, поэтому согласно (2.28) до,

I; i = j;

(2.29)

Методы решения систем линейных алгебраических уравнений разделяются на точные и итерационные. Точные методы дают решение системы линейных уравнений после конечного числа арифметических операций. Однако использование точных методов, например метода Гаусса, осложняется большим временем счета на ЭВМ, пропорциональным порядку системы в кубе [2.12]. Так, например, для решения одной системы линейных уравнений порядка 1000 на ЭВМ средней мощности требуется более 10 ч машинного времени.

Главное достоинство итерационных методов состоит в том, что для них время счета на ЭВМ пропорционально порядку системы в квад. рате [2.12]. Среди итерационных методов решения систем линейных уравнений в последние годы получил широкое распространение метод блочных итераций (модификация метода Гаусса - Зейделя для-случая клеточных матриц).

Рассмотрим решение методом блочных итераций системы линейных алгебраических уравнений

(2.30)

Идея метода состоит в следующем. Матрица коэффициентов, системы разбивается на Р прямоугольных клеток Ац (г, у=1, 2, ..., /). Размерность каждой клетки матрицы А, равна пцХт причем

т: =п.

Соответствеино векторы свободных членов вихревой составляющей напряженности поля ;i неизвестных Y разбиваются на / векторов Н^. и Yi размерности (.

Тогда система (2.30) сводится к системе / клеточных уравнений: Aiiii + AiV, + ... + AuYi = HI,; 2Уг + А^Л + . + А,гУ г = Я ;

lгYг + нY, + ... +A,iYi=Hli. Общая формула вычисления й-го приближения вектора У/* имеет вид / <-1 ;

Yf = АТТ'

с^-2ЧУ/- S А,/1Г*-)(=1,2....,/). <2.31)

1=1 ii+i /

ё

Дли кйзкдогО приближения вектора У* точным методом вычисляется Только обратная матрица AJj. Перед началом Счета по формуле (2.31) необходимо задаться начальными приближениями векторов У^ (t=l, 2.....I).

Для оценки устойчивости интегральных уравнений (2.20) и (2.21) рассматривалась устойчивость аппроксимирующих их систем линейных алгебраических уравнений (2.30). С этой целью рассчитывалось число обусловленности матрицы А по формуле

с=А|А-Ч1, где А|= maxSlaj/l-норма матрицы А.

Относительная погрешность решения системы линейных алгебраических уравнений удовлетворяет неравенствам

8У

;ИАО (2.32)

£11ЯеГ HiII II АII

Из неравенств (2.32) видно, что чем больше с, тем система линейных алгебраических уравнений менее устойчива. Значение с-гораздо более важный критерий устойчивости решения системы линейных алгебраических уравнений, чем малость определителя А или большой порядок системы.

Для различных КЭМ расчеты показали, что с находятся в диапазоне от 10 до 30 (например, в криогенном генераторе мощностью 200 кВт получилось с=15).

Как показали результаты итерационного решения системы линейных алгебраических уравнений с с= 10--30, небольшая погрешность, возникающая при вычислении вихревой составляющей напряженности магнитного поля ЦбЯсЦ и замене интеграла конечной суммой ЦбАЦ, может привести к тому, что решение либо получается физически неверным, либо расходится.

Для повышения устойчивости приближенного решения интегрального уравнения Фредгольма второго рода часто используется метод регуляризации А. Н. Тихонова [2.13], заключающийся в следующем. Если в правой части интегрального уравнения (2.9) имеется элемент /пр(л:), уклоняющийся ОТ точной правой части f-r{x) не более чем на г\, ТО приближенное решение Ynp{x) интегрального уравнения определяется с помощью регуляризующего оператора, зависящего от параметра. Значение параметра выбирается

согласованным с погрешностью ц исходных данных fnp(x), чтобы /пр(х)-/т(л:), Упр(л:)-Ут(л') при Т1-0.

Повышение устойчивости интегральных уравнений (2.20) и (2.21) методом регуляризации рассмотрено в [2.2], где в качестве дополнительных условий использовались равенства нулю сумм поверхностных и объемных магнитных зарядов соответственно на поверхности и в объеме ферромагнетика. Так как в КЭМ распределение вихревой составляющей напряженности магнитного поля является симметричной функцией, то при решении интегральных уравнек.чй (2.20) и (2.21) указанные суммы плотностей всегда равны нулю. Однако это не позволяет полностью устранить неустойчивость от погрешности вычисления вихревой составляющей напряженности магнитного поля, так как остается неустойчивость вследствие погрешности от замены интеграла конечной суммой. Рассмотрим подробно причины неустойчивости интегральных уравнений (2.20) и (2.21) [2.14J.

Если ферромагнитный экран намного длиннее обмотки возбуждения, то при (Хгэ=оо магнитное поле полностью экранируется и, следовательно, распределения плотностей поверхностных магнитных зарядов на поверхностях 5; {i= =2, 3) равны нулю (см. рис. 2.3). Примем эти распределения за начальное приближение векторов У°,=0 {i==2, 3)-

Из (2.31) уже на первой итерации должны получиться точные значения векторов Kl и К'2=К'з=0. В расчетном выражении вектора

yI = {/ili - Ai.Au ?,) {i--=2, 3) (2.33)

заключенная в скобки часть должна равняться нулю, но из-за погрешности вычислений равенство не наблюдается.

Это приводит к неустойчивости решения системы (2.30). Анализ (2.33) показывает обе причины неустойчивости: неточность вычисления вихревой составляющей напряженности магнитного поля Я^с; неточность замены интеграла конечной суммой и приближенное вычисление обратной матрицы.

Чтобы сделать систему линейных алгебраических уравнений сходящейся для любого гэ, заменим вектор Я^с; {i=2, 3) на близкий к нему вектор:

А,-,Ап Яс1 (/ = 2,3),

(2.34)

рассчитанный при (х^э=оо-

Такая замена дает возможность получить у^2==У^з=0

при 1гэ=оо, что позволяет полностью устранить неустойчивость, возникающую от указанных причин.

Приближенное решение интегрального уравнения Яс.пр (2.30) с измененной правой частью на поверхностях St {i=2, 3) по формуле (2.34) стремится к искомому точному решению Н^с,т, потому что с уменьшением погрешности ц вычисления вектор Яс,пр-* Яс,т-С ростом порядка системы

линейных уравнений я векторы Hi Н^.т {1=2, 3).

Для недостаточно длинного ферромагнитного экрана, частично экранирующего магнитное поле, сначала определяем плотности магнитных зарядов на поверхности S\, предполагая полное экранирование. Затем по (2.34) рассчитываем Н'ы на поверхности 5,- {1=2, 3) реального экрана.

Для повышения устойчивости интегрального уравнения (2.21) внутри ферромагнитного экрана заменяем вектор

Я^с на вектор Я'с, рассчитанный также по (2.34) при

Рассмотрим итоги расчета трехмерного магнитного по-. ля в КЭМ с нелинейным изотропным ферромагнитным экраном на примере статической модели криогенного генератора [2.14]. В этой модели сверхпроводниковая система возбуждения имеет две седлообразные катушки по 2500 витков. Криостат снаружи охвачен сплошным ферромагнитным экраном из материала Ст. 10 (рис. 2.4).

Магнитное поле измерялось на внутренней поверхности ферромагнитного экрана, а также на среднем диаметре обмотки возбуждения в ее центре и на внутренних витках в зоне лобовых частей обмотки. Расположение датчиков на внутренней поверхности экрана показано на рис. 2.4.

Расчет магнитного поля и его измерение на модели криогенного генератора проводились при двух токах возбуждения /в. При /в=25 А ферромагнитный экран был не насыщен, а при /в=70 А-сильно насыщен, что позволило проверить разработанный метод расчета магнитного поля в КЭМ при разных состояниях ферромагнитного экрана. - Степень насыщения ферромагнитного экрана оценивалась по отношению радиальной составляющей магнитной индукции, измеренной на внутренней поверхности ферромагнитного экрана, к радиальной составляющей магнитной индукции, измеренной в тех же точках, но без экрана.

Расчет магнитного- поля в статической модели криоген-