s,+s.

*3л

dSN =

( °-+ °)gradH. 4ян-ГЭ

(2.44)

Численное решение интегральных уравнений (2.42) и (2.44) проводится по алгоритмам, изложенным в § 2.3.

Рассмотрим особенности решения интегрального уравнения (2.43). Так как численное интегрирование по поверхности 5зл всех л листов ферромагнитного экрана требует гораздо большего числа разбненнй, чем допускают расчеты на современных ЭВМ, разобьем объем ферромагнитного экрана на Мл эквивалентных листов. Толщина эквивалентного листа и толщина эквивалентного изоляционного промежутка между листами составляют

Дл = /э/Сс1/Л1л; Ди =(1-Д:ст)/э/Л1л,

где h - длина ферромагнитного экрана.

Каждый нз Мл листов ферромагнитного экрана разобьем на Кя элементов объема ДУэ с площадью боковой поверхности Д5з. Приняв постоянной плотность поверхностных магнитных зарядов Ст2м на поверхности Л5з, соответствующий интеграл в (2.43) представим в виде конечной суммы

2п

QAf3 Q

QNЗmQ

AS3, (2.45)

где Л^т - точка в центре боковой поверхности as3.

Проанализируем случай когда при численном интегрировании по 1(2.45) точка Q совпадает с точкой Л^п (см. рис 2.3). Напряженность

магнитного поля в точке Л' от магнитных зарядов поверхности Д5 равна нулю, так как Гдг д, =0. Можно считать, что магнитное поле между поверхностями Д5з и Д54 одного листа аналогично электрическому полю плоского конденсатора. Тогда в точке Nn напряженность магнитного поля, создаваемая магнитными зарядами поверхности ASi, равна

fiN = - ш (Л^ )/2.ао. (2.46)

п

Используя (2.46), преобразуем квадратурную формулу (2.45), к виду

2п

2п

S

т=1 \

.1 jj

2м(Л^..7)

п зт п

N N,

2м(Л^т)

Д5я =

2п

т=п + \

п 4т Г

USs. (2.47)

С учетом (2.47) коэффициенты системы линейных уравнений, аппроксимирующей интегральное уравнение (2.43), имеют внд

1 -

2. 1

о

N N.

Д5з; пфт.

Решив систему интегральных уравнений (2.42) - (2.44) и иайдя распределение плотностей поверхностных OiM и а2м и объемных р„ магнитных зарядов, рассчитаем потенциальную составляющую напряженности магнитного поля:

uSk -

Результаты совместного решения (2.42) - (2.44) показывают, что практически при расчете магнитного поля в КЭМ можно пренебречь поверхностными магнитными зарядами Огм.

Подход, основанный на приведении шихтованного ферромагнитного экрана к фиктивному анизотропному экрану с взаимно перпендикулярными осями анизотропии, не позволяет точно рассчитать магнитное поле за экраном и, следовательно, определить потери в корпусе и других конструктивных элементах статора. Для иллюстрации сказанного рассмотрим расчет магнитного поля на наружной поверхности шихтованного ферромагнитного экрана, когда 1гэ=оо. В этом случае анизотропный экран с взаимно перпендикулярными осями анизотропии в радиальном и азимутальном направлениях имеет относительную магнитную проницаемость Цгд=1га=Ргэ=оо. Тогда, как и в изотропном ферромагнитном экране с ргз=оо, радиальная составляющая магнитной индукции на его наружной поверхности будет равна нулю. Магнитная индукция на этой поверхности не равна нулю при ргэ=оо вследствие краевого эффекта вокруг каждого листа. В разработанном подходе краевой эффект (шихтовка) учитывается не только в уравнении (2.43) для плотностей поверхностных магнитных зарядов Огм, но также в уравнениях (2.42) и (2.44) для плотностей поверхностных Ош и объемных р„ магнитных зарядов. В (2.42) и (2.44) параметры уравнения равны соответственно А,/Сст/2я и /Сст/4яргэ. При ргэ=оо (А,=1) плотность на наружной поверхности ферромагнитного экрана а1фО, так как коэффициент заполнения КстФ, но р„=0 внутри Уэ, поскольку /Сст/4яргэ=0 при ргэ=оо. Отсюда следует, что на наружной поверхности шихтованного ферромагнитного экрана магнитное поле больше, чем на поверхности нешихтованного экрана.

В криогенном генераторе мощностью 200 кВт магнитное поле на наружной поверхности ферромагнитного экрана (рис. 2.7) рассчитывалось и определялось экспериментально.

При расчете численно решалась система уравнений (2.42) -(2.44). Использовалось также число разбиений ферромагнитного экрана и обмотки возбуждения, как при расчете магнитного ноля модели криогенного генератора (см. рис. 2.4). 72

Ж

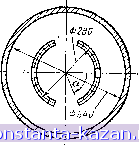Рис. 2.7. Основные размеры криотурбогенератора мощностью 200 кВт

Расчетные и измеренные значения магнитной индукций на наружной поверхности шихтованного ферромагнитного экрана при токе возбуждения /в=80 А сопоставлены на рис. 2.8,а, из которого видно, что их различие не превосходит 7%. На этом же рисунке даны для сравнения значения магнитной индукции, рассчитанные без уче/а шихтовки ферромагнитного экрана. Погрешность этих расчетов больше: отклонение от данных измерений получается до 30% в сторону уменьшения индукции. Распределения относительной магнитной проницаемости внутри ферромагнитного экрана, рассчитанные при токе возбуждения криогенного генератора /в=80 А с учетом и без учета шихтовки экрана, показаны на рис. 2.8,6.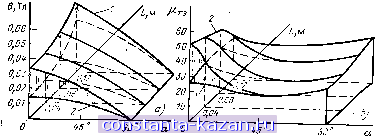

Рис. 2.8. Распределения радиальной составляющей магнитной индукции на поверхности экрана (а) и магнитной проницаемости внутри экрана (б):

- расчет с учетом шихтовки ферромагнитного экрана: 2 -то же без учетя шихтовки (*-эксперимент) ,~ л

2.5. Расчет вихревых токов в ферромагнитном экране

Рассмотрим в общем виде метод расчета составляющей напряжевности магнитного поля созданной вихревы-

ми токами в ферромагнитном экране.

Интегральные уравнения для расчета трехмерного квазистационарного магнитного поля в объемно-неоднородной проводящей ферромагнитной среде приведены в [2.2].

Плотность вихревых токов в проводнике определяется по формуле

]=уЁ=-1&уЛ (2.49)

где А-векторный потенциал; Ё-напряженность электрического поля; 7э-удельная электрическая проводимость; (о-угловая скорость.

Чтобы перейти к системе интегральных уравнений для расчета плотности вихревых токов в объемно-неоднородной проводящей ферромагнитной среде, требуется выразить векторный потенциал через комплексные вторичные источники: векторные - объемные Jo,h и поверхностные Уп.н плотности токов намагниченности, скалярные - объемные р„ и поверхностные Ом плотности магнитных зарядов.

Векторный потенциал А от векторных вторичных источников определяется однозначно, а от скалярных-с точностью до градиента гармонической функции [2.2]. Следовательно, плотность вихревых токов j при решении интегрального уравнения с векторными вторичными источниками определяется однозначно, а со скалярными-неоднозначно.

Векторные вторичные источники определяются несколькими скалярными: поверхностная плотность тока ja,h-двумя, а объемная плотность тока Уо,н-тремя скалярными функциями. Следовательно, одно интегральное уравнение, содержащее векторные вторичные источники, равносильно двум или трем интегральным уравнениям, содержащим скалярные источники.

При использовании векторных вторичных источников, а не скалярных, приходится решать систему из пяти интегральных уравнений вместо двух. Это приводит к значительному увеличению времени численного решения на ЭВМ. таких интегральных уравнений. Во избежание указанных затруднений расчет квазистационарного магнитного поля в объемно-неоднородной проводящей ферромагнитной среде будем проводить-следующим образом [2.15].

Для каждой компоненты плотности вихревого тока J {i=x, у, z) разобъем весь проводящий массив Уъ на Мв элементов объема АУэ при следующих допущениях:

1) плотность вихревого тока j, {i=x, у, z) в каждом элементе объема АУэ постоянная по величине и фазе;

2) на границе массива Уэ, перпендикулярной компоненте i, плотность вихревого тока ji=0 на расстоянии, равном половине шага разбиения.

Второе допущение обосновывается тем, что на границе нормальная компонента плотности вихревого тока равна нулю. В связи с этим расчеты будут выполняться тем точнее, чем меньше шаг разбиения.

На рис. 2.9 показано, как проводится разбиение прово^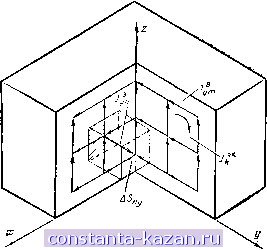

Рис. 2.9. Схема разбиения проводящего массива объемом У прн расчете вихревых токов

дящего массива Уэ. Если провести прямые через центры всех элементов объема АУэ в направлении соответствующих осей координат, то в трехмерной постановке задачи получится пространственная решетка.

Согласно первому закону Кирхгофа в узлах решетки сумма плотностей тока равна нулю. Учитывая замкнутость линии тока, вместо реальных плотностей вихревого тока jim будем определять плотности эквивалентных вихревых токов /ft3K замыкающихся по контуру L, состояще-