функционала для комплексных амплитуд пространственных гармоник с использованием двумерных конечных элементов и минимизации функционала, учитывающего наличие вихревых токов на поверхности проводящей среды, с использованием одномерных конечных элементов.

Метод интегральных уравнений. Математическая теория интегральных уравнений дана в [2.11].

В общем случае линейное интегральное уравнение имеет вид

0{х)У{х) + Л„ f К{х, z)Y{z).dz = f , Г2.9>

где У (.г) - искомая функция; свободный член f(x), ядро уравиеиия К{х, г) н коэффициент G(x)-известные функции; Яи- параметр интегрального уравнения; D - область интегрирования.

Интегральное уравнение (2.9) называется уравнением первого рода, если G{x)=0 для xsiD, и уравнением второго рода, если G(x)=H=0 для всех xD. Интегральное уравнение называется уравнением Фредгольма, если ядро К{х, г) в уравнении (2.9) вполне непрерывно, и уравнением Вольтерра, если ядро К(х, z) в (2.9) обращается в пуль при г>х.

Для численного решения интегральных уравнений наиболее часто используются следующие методы: метод квадратурных формул, метод Вырожденных ядер, метод последовательных приближений [2.11].

Впервые метод интегральных уравнений для аналитического расчета магнито- н электростатических полей в кусочно-однородных линейных средах предложил Г. А. Гринберг. В [2.2] выполнено дальнейшее развитие метода интегральных уравнений, получены интегральные уравнения для электро- и магнитостатических полей, а также для вихревых токов в неоднородных, анизотропных и нелинейных средах.

По методу интегральных уравнений влияние неоднородной среды учитывается вторичными источниками, которые вводятся всюду, где меняются характеристики среды. Это позволяет привести систему уравнений, описывающую поле в неоднородной среде, к системе, описывающей эквивалентное поле в вакууме. Расчет магнитного поля сводится к нахождению распределения вторичных источников путем решения системы интегральных уравнений Фредгольма второго рода относительно плотностей вторичных источников. Далее легко определяется индукция магнитного поля.

2.2. Расчет магнитного поля в однородной среде

Как указывалось, чтобы в однородной среде с магнитной проницаемостью ло создать магнитное поле, эквивалентное магнитному полю в КЭМ, необходимо на поверхности и в объеме ферромагнитного экрана йвести вторичные источники. Наиболее эффективно Для учета на-

магниченности ферромагнитного экрана вводить скалярные вторичные источники, а не векторные: одно интегральное уравнение, содержащее векторную функцию, равносильно двум или трем уравнениям, содержащим скалярные функции. Таким образом, для учета намагниченности ферромагнитного экрана в КЭМ целесообразно использовать фиктивные поверхностные и объемные магнитные заряды. В этом случае вектор результирующей напряженности магнитного поля можно представить как сумму

(2.10)

где Я^ - вихревая составляющая от токов в катушках; Дв.э - .J.Q jjg QJ вихревых токов в экране; Я -потенциальная составляющая, созданная фиктивными поверхности ными и объемными магнитными зарядами.

Согласно закону Био-Савара-Лапласа находим

H>.Q-lj±iSydV (2.11)

где гд,у - расстояние между точками наблюдения Q и ис-

. точника поля N.

Чтобы повысить точность и сократить время расчета на ЭВМ Й * по (2.11), необходимо уменьшить объем вычислений, приходящихся на долю численного интегрирования, и увеличить вклад аналитических преобразований. С этой целью катушки сложной конфигурации разбиваются на простейшие элементы: дуги круговых витков, отрезки прямых проводников, прямоугольные призмы и др., магнитное поле которых может быть рассчитано аналитически. Поле катушки получается суммированием магнитных полей элементов разбиения.

Один из универсальных алгоритмов расчета напряженности магнитного поля обмоток сложной конфигурации основан на замене витка с током прямолинейными отрезками [2.14]. Например, сечение катушки ,(рис. 2-2) разбиваем на Р элементов площадью ASp, каждый из которых заменяется тонким витком, РисГ2.2. Схема разбиения катуш-Проходящим через центр ки- иа элементарные витки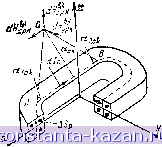

элемента. По витку р протекает ток Л/р=/рЛ5р (/р - плотность тока). Теперь отдельный виток заменим К прямолинейными отрезками. На основании (2.11) вычислим напряженность магнитного поля в произвольной точке Q от отрезка k витка р;

Д Я^ (Q) = - /р (cos а ; + cos а,р,)/4ад , (2.12)

где apft -расстояние по нормали от точки Q до отрезка к витка р; aiph, a2ph - внутренние углы, образованные отрезком k витка р и двумя векторами, проведенными из концов этого отрезка в точку Q.

Суммируя эти составляющие по всем К элементам для всех Р эквидистантно проходящих ломаных линий, получаем

r(Q)=S SA(Q).

где i~x, у, г -индексы соответствующих проекций трех-X мерного вектора.

При расчете распределения поля в толще катушки точки Q надо задавать в узлах сетки разбиения, чтобы избежать математической особенности в случае apk=0. Значения напряженности магнитного поля в промежуточных точках определяются путем интерполяции.

2.3. Расчет магнитного поля с учетом нелинейности ферромагнитного экрана

Для расчета потенциальной составляющей напряженности магнитного поля Я в качестве вторичных источников внутри ферромагнитного экрана вводятся объемные магнитные заряды, а на поверхности ферромагнитного экрана вводится простой слой поверхностных магнитных зарядов.

Рассмотрим вывод системы интегральных уравнений для определения плотностей поверхностных и объемных магнитных зарядов [2.2]. С этой целью запишем уравнение

divfi =div [Хд;а^з = [ipffi-jdivW -fTgrad a,) = О, из квтерого получим

div/f- --( grad,s)/H.,s, <2.13)

we .Цгэ - отиосйтельнай магвмтмай проницаемость ферромагнитйого экрана.

Плотность объемных магнитных зарядов в точке Q

Pm(Q) = - li>-ofi iQ) grad w-r э]¥г э-Плотность поверхностных магнитных зарядов

(2.14)

5м == lim Р.м'.

h-*0

(2.15)

где ft -толщина слоя, в котором распределен магнитный заряд с объемной плотностью рм-

Среднее значение градиента цхгэ в слое толщиной h

(grad Мер = (1Аг.-1)п7Л, (2.16)

где я - единичный вектор нормали к поверхиости ферромагнетика.

Среднее значение относительной магнитной проницаемости в этом слое

[-.Р=(1+.-э) 2. Подставив (2.16) и (2.17) в (2.15), получим:

iM(Q) = 2p. X (Q) ,

(2.17)

(2.18)

где )=(Хгэ-1)/(1гэ--1).

Вектор напряженности магнитного поля выразим посредством плотностей поверхностных и объемных магнитных зарядов:

H(Q) = (Q) + (д) + fiHQ) =

f p ()JdF-f({)o (iV)-dS,

Подставив (2.19) в (2.14) и (2.18), получим систему интегральных уравнений Фредгольма второго рода для определения неизвестных плотностей поиерхностных и объемных магнитных зарядов:

4jc,u.o

m(Q) +

2п

Pm(Q)

4nti.

(2.20)

grad (j.

.л

в к вэ -

где , ff - нормальные проеквди вихревых составляющих напряженности магнитного поля.

Относительная магнитная проницаемость экрана Цгэ зависит от напряженности магнитного поля и определяется свойствами материала, что делает систему интегральных уравнений (2.20) и (2.21) нелинейной.

В результате совместного решения уравнений (2.20) и (2.21) на основе найденного распределения плотностей поверхностных и объемных магнитных зарядов по (2.19) определяется потенциальная составляющая напряженности магнитного поля ff (Q).

Метод последовательных приближений позволяет свести решение системы нелинейных интегральных уравнений (2.20), (2.21) к последовательному решению линейных интегральных уравнений по следующему алгоритму.

1. Рассчитывают предварительное распределение р-э-С этой целью находят результирующую напряженность магнитного поля на внутренней поверхности ферромагнитного экрана

Н„ = 2{НГ +НГ). (2.22)

Расчет по (2.22) дает значение An, завышенное примерно на 20-30%. Интегрируя Йп по внутренней поверхности, определяют магнитный поток Ф, входящий в экран. Зная Ф и принимая допущение, что магнитная индукция постоянна по толщине экрана, определяют распределение магнитной индукции в ферромагнитном экране. Затем рассчитывают lira .

2. Рассчитывают плотность поверхностных магнитных зарядов ам\ решив интегральное уравнение (2.20). [При первом решении интегрального уравнения (2.20) плотность объемных магнитных зарядов рм принимается равной нулю.]

3. Определяют плотность объемных магнитных зарядов р„, решив интегральное уравнение (2.21).

4. Находят результирующую напряженность магнитного поля Н внутри ферромагнитного экрана, а по ней уточняют распределение \хгэ'.

5. Рассчитывают относительные погрешности вычисле

ния плотностей поверхностных Ва и объемных ер магнитных зарядов:

е„=ам-ам-Ч1/11а 11; (2.23)

ер=р„-р„-1/11рмЯ1, (2.24) ;

где выражение типа ЦХЦ ==тах jX/l обозначает норму

вектора X.

Если погрешности Sa и Ер не превышают допустимых пределов, то расчет оканчивается, в противном случае необходим возврат к п.2.

Для численного решения линейных интегральных уравнений эффективен метод квадратурных формул [2.И], при использовании которого интеграл в уравнении (2.9) заменяется конечной суммой:

п

\К(Х1, x)Y(x)dx = ajKiXi, Xj)Y(x,) + R{K(xt, x)V(x)]. (2.25)

Ъ /=1

Здесь О] - коэффициенты, зависящие от выбора квадратурной формулы; R[K[xu х)У(х)] - остаточный член.

Отбросив остаточный член квадратурной формулы и подставив выражение (2.25) в линейное интегральное уравнение (2.9), получают систему линейных алгебраических уравнений ft.

Y(xi) + K aiKiXi, xi)Y(Xi)=f(M) (i = 1, 2,..., n). (2.26)

Решение (2.26) дает значения t{Xi) (i=l, 2.....л), по которым

путем интерполяции находят приближенное решение интегрального

уравнения в любых точках области.

При решении методом квадратурных формул интегрального уравнения (2.20) целесообразно поверхность ферромагнитного экрана разбить на три гладкие поверхности Sk, k=\, 2, 3 (рис. 2.3). Для решения интегрального уравнения (2.21) объем ферромагнитного экрана разбивают на L слоев так, чтобы поверхность, проведенная через центры элементов объема каждого слоя, была, цилиндрической. В этом случае функции a {x) на поверхности Sk и рм{х) в каждом слое будут гладкими.

Ядра интегральных уравнений (2.20) и (2.21) не ограничены при совпадении точек Q и Л^, т. е. имеют математические особенности. Эти особенности слабые, так как ядра можно представить в виде

К (Q, л^)=(Q, л^)/г- (О <>:< М„),

где F{Q, Л^)-ограниченная функция; Мп - размерность пространства.