ки £], так как падение напряжения иа омическом сопротивлении весьма мало; поэтому

t/, = £-i + /rri = a-

Подставляя в выражение (б) Eiz=Ui, /=50 гц и k=z0,9, получим:

откуда следует:

6,. 108

Найдем далее площадь сечения окна Qo, занимаемую обмотками трансформатора.

Точное определение площадп, занимаемой обмотками, возможно лишь после окончания расчета трансформатора, когда известны количество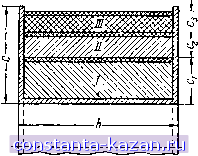

Фиг. 23. Катушка трансформатора в разрезе.

витков и диаметр провода для каждой нз обмоток. Поэтому найдем приближенное значение площади обмоток, с тем чтобы в дальнейшем проверить размещение обмоток в окне сердечника. Из фиг. 23 очевидно, что

где Qi, Q,3 9з, -площади, занимаемые отдельными обмотками с учетом всех прокладок и каркаса.

Если трансформатор содержит п обмоток, то выражение (д) принимает BUV

Qo = Qi + Q-QB + --- + Qn- (е)

Выразим площадь, занимаемую первичной обмоткой трансформатора Qi, следующи.л образом:

площадь сечения провода первичной обмотки в мМ;

- коэффициент заполнения окна трансформатора медью, учитывающий изоляцию провода, прокладки между обмотками, а также неплотность намотки.

В то же время известно:

где /] - ток первичной обмотки; Д -плотность тока.

Поэтому

1 = lOkJi.

или, подставив сюда значение t j из формулы (г), получим:

10* /it/i

Но Jit/= - мощность первичной обмотки трансформатора в ва, следовательно:

Это выражение справедливо для любой из обмоток трансформаторя, если в качестве Р подставлять вольтамперы данной обмотки:

10* Pg[sa]

Величины ft H Д для всех обмоток принимаем одинаковыми. Найдем

теперь площадь окна Q, подставив полученный результат в выражение (/):

104 1

(? = (?1 + + . . . + С? -g-20-- (Р,1-Ь Ра-Ь . . .-Ь р„) (л)

Суммарная мощность вторичных обмоток р2-Ь Рз-Ь-. .-f д =-Рц связана с мощностью первичной обмотки Pj через к. п. д. трансформатора Yjy.:

Подставив последнее выражение в формулу (л), получим:

104Я„(1+ )

или окончательно:

Итак, мы пришли к выражению, которое показывает, что при заданной мощности Р„ мы должны иметь сердечник с произведением QQo не менее определенной величины.

Приложение 4

ВЫВОД ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ ЧИСЛА ВИТКОВ ДРОССЕЛЯ, РАБОТАЮЩЕГО С ПОСТОЯННЫМ ПОДМАГНИЧИВАНИЕМ

Индуктивность дросселя с сердечником из магнитного материала при наличии зазора в сердечнике может быть найдена по известной формуле

4j:-w2.q .ft

где L - индуктивность, гн;

W - число витков обмотки дросселя;

- сечение сердечника, см;

- коэффициент заполнения сердечника, учитывающий изоляцию пластин и неплотность сборки;

1 - длина средней магнитной силовой линии в сердечнике, выраженная в см;

ft - динамическая проницаемость материала сердечника; /j -длина зазора, см.

Эту формулу можно представить в таком виде:

=-l-W Здесь л' - эквивалентная магнитная проницаемость сердечника с учетом зазора

Однако приведенное выше выражение для L не позволяет непосредственно определить количество витков обмотки дросселя по заданной индуктивности, так как магнитная проницаемость и наивыгоднейшая величина зазора при работе дросселя с подмагничиванием зависят от числа витков W. Эти зависимости обычно задаются графически, что 9начител|>но затрудняет расчет.