3 Вентили Д1 и Дг имеют бесконечно большое обратное и нулевое прямое сопротивления

4 Активное сопротивление и индуктивность рассеяния рабочих обмоток равны нулю

Пусть О^м/л; является оабочим полупериодом сердечника Л (вентиль Д.1 открыт), его индукция в начале полупериода (определяется напряженностью поля управляющего сигнала i/y=

=/у-у-)на статической пегле гистерезиса равна ВуА, а в сердечнике Б равна индукнии насыщения

В интервале возбуждения сердечника А, пока он не насыщен, в результате изменения индукции в его обмотке управления индуцируется ЭДГ, которая суммируется с напряжением сигнала управления и прикладывается к обмотке управления сердечника Б. В результате в сердечнике Б его обмоткой управления возбуждается переменное магнитное поле Для цепи управления справедливо соотношение, совпадающее с выражением (2 И)

yS- + yS + hRy-r (2.14)

При условии, что /?у->0 также выполняется и равенство (2.2). На интервале возбуждения сердечника А для рабочей цепи справедливо уравнение

. . WpS + Ri ,==Us\xi.&t, , (2.15)

в кЬтором, как правило, молено пренебречь величиной намагничивающего тока гихх, оп0еделяемой как

Тогда, интегрируя (2 15) jc учетом (2 2) и Ihxx=0. получим выражения для закона изменения индукции в сердечниках, совпадающие с (2 5) и (2 6)

a = 5yA + 6m(l-COSCuO, Вб = £5-5(1 -COS СО/),

где Bm=UJ((,)WpS)

В отличие 01 дроссельных МУ в рассматриваемом МУ перемагничивание сердечника Б на интервале возбуждения осуществляется не рабочей обмоткой (ipB =0), а обмоткой управления Для интервала возбуждения характерно быстрое перемагничивание сердечников, поэтому индукция в них изменяется по динамическим петлям* гистерезиса

На основании закона полного тока для сердечника Б па интер ьале возбуждения может быть определен ток управления

Если положить .1д = со. то на интервале возбуждения ток ур--равления будет неизменным

1у = -

сД = ~сД

: const.

(2.17)

В момент /= /м индукция в сердечнике А достигает значения Bs и в дальнейшем не изменяется. В обмотках трансформатора А ЭДС не индуцируется. Поэтому величина индукции в сердечнике Б будет определяться напряженностью управляющего сигнала иа статической петле гистерезиса. На основании закона полного тока для сердечника Б на интервале насыщения можно определить величину iy

fB = - fc

+ Bg/гдг„ = гyШy/z,

lд

При !.1д = оо

iy = - (l/Wy) H = ~I const. (2.18)

В отличие от дроссельных МУ на интервале насыщения сердечника А рабочая обмотка сердечника Б отключена вентилем До от источника питания. Поэтому ток из рабочей цепи уже не будет трансформироваться в цепь управления, т. е. полностью устраняется отрицательная ОС характерная для дроссельных МУ.

Выражения для угла насыщения, мгновенного и среднего значений тока нагрузки совпадают с соответствующими выражениями для дроссельных МУ.

Среднее значение тока управления в интервале О^Ы^л в соответствии с выражениями (2.17) и (2.18)

-о а

(2.19)

Относительная величина среднего значения тока нагрузки в соответствии с выражениями (2.9), (2.9а) и (2.19) (без учета намагничивающего тока /iioix) .может быть представлена в виде

Выражение (2.20) справедливо при -/сд/у^-/с Действительно, при /у>-1с установившееся значение магнитной индук-

ции равно индукции насыщения, т. е. сердечники находятся в насыщении в течение всего периода, поэтому ток нагрузки равен максимальному значению. Минимальное значение тока нагрузки имеет место при /у = -/сд.

Из выражения (2.16) для намагничивающего тока с учетом соотношения (2.17) при [1д=оо имеем

4хх = 2 ,д( Шр).

среднее за полупериод значение намагничивающего тока зависит от величины угла насыщения

/нохх = 2(а/я)Я,д(/Н). (2.21)

Подставляя в выражение (2.21) а=я, найдем минимальное значение тока нагрузки

4от/ = 2( едг/Шр) = 2/ед. (2.22)

Выражения (2.20) и (2.22) определяют характеристику управления МУ с внутренней ОС.

Характеристика управления МУ на реальных середечниках отличается от идеальной (рис. 2.11). На рис. 2.12 представлена экс-

ио/на max . ,.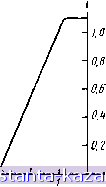

-f -2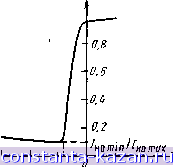

-15 -10 -5

5 W Iy мА

Рис. 2Л Г. Характеристика управления МУ с внутренней обратной

связью (Ясд/Яс = 3 и

аЯсдг/р/н<,т п=!0,7).

Рис. 2.12. Экспериментальная характеристика МУ с внутренней обратной связью

периментальная характеристика управления МУ, выполненного на сердечниках из желозоникелевого сплава 50НП. Наиболее существенное отличие характеристик рис. 2.11 и рис. 2.12 заключается в том, что ток нагрузки меньше /нотах в отсутствие входного сигнала. Это объясняется тем, что рабочие обмотки обладают как активным, так и индуктивным сопротивлением при насыщении сердечников ((is>0).